우리가 이제까지 배운걸 한 덩어리로 뭉치면 Linear Classifier가 만들어집니다. 입력값 X와 임의의 가중치 W, Score function, Loss function, 그리고 Regularization term으로 이루어진 덩어리였습니다. 우리는 이를 학습시켜 loss가 가장 낮게 나타나는 W값을 찾는 것이 목표였습니다. 이 과정을 도식화하면 다음 하나의 그림으로 나타낼 수 있습니다.

Why backpropagation?
학습을 통해 최적의 가중치 W를 찾고 싶다는 건 이제 알겠습니다. 이제까지 우리가 그려온 대로 저런 단순한 식이라면 가중치를 학습시키는게 크게 어렵지 않을 것입니다. 그러나 앞으로 우리가 배울 것들은 이런 단순한 모델이 아닙니다.
예를 들면

이런 거라던지
이런 끔찍한 것들입니다
이처럼 파라미터가 매우 많고 여러 개의 레이어로 구성되어 있다면 기존의 방식들로는 학습이 어렵습니다. 그래서 새로운 방식을 적용합니다. 각 레이어별 기울기를 구하고 그 기울기를 이용해서 경사 하강법을 적용하면 가중치 W를 update 시켜 나가며 학습시킬 수 있습니다. 이때 역전파 알고리즘을 활용합니다.
미분값은 한 지점에서의 기울기를 나타냅니다. 이는변화하는 정도를 보여주죠. 즉 우리는 미분을 통해서 해당 노드가 loss에 미치는 영향을 알 수 있습니다.
역전파 알고리즘(Back propagation)
우선 우리가 하고자 하는 것을 명확히 하고 넘어가겠습니다. 우리는 각 노드(아래 그림의 x, y, z,)가 출력 노드(아래 그림의 f)에 미치는 영향력의 크기를 알고 싶은 것입니다(미분을 하는 이유를 생각해 보세요!). 이를 이해하면 지금부터의 과정을 보다 직관적으로 이해할 수 있습니다.
우리가 설계한 모델의 최적의 W를 구하기 위해 우선 임의의 W값과 각 노드별 정답 값을 가지고 순방향으로 나아가며 계산합니다(그리고 이 과정 속에서 우리는 local geadient를 얻습니다. 기억해두세요!). 최종적으로 우리는 loss값을 얻습니다. 이 loss는 임의로 설정한 W를 바탕으로 도출되었기 때문에, 우리는 최적의 값을 찾기 위해 W값을 지속적으로 update 시켜야 합니다.
가중치값을 지속적으로 update 해줘야 하는 것은 알겠습니다. 그러나 마구잡이로 update 하는 것은 너무 비효율적이겠죠? 보다 효과적으로 가중치를 조절하기 위해 우리는 미분을 사용합니다(큰 영향을 미치는 것은 크게, 또 부정적인 영향을 미치는 것은 작게!). 그러나 이 과정에서 우리는 각 노드들의 W값의 기울기를 구하기 위해서 또다시 많은 연산을 수행해야 합니다. 이 문제를 역전파 알고리즘을 통해 해소할 수 있습니다. 역전파 알고리즘은 Computational graph를 그려서 생각하면 이해하기 좋습니다. 우리가 이번에 볼 예제는 사실 이 한 장으로 요약 가능하죠.
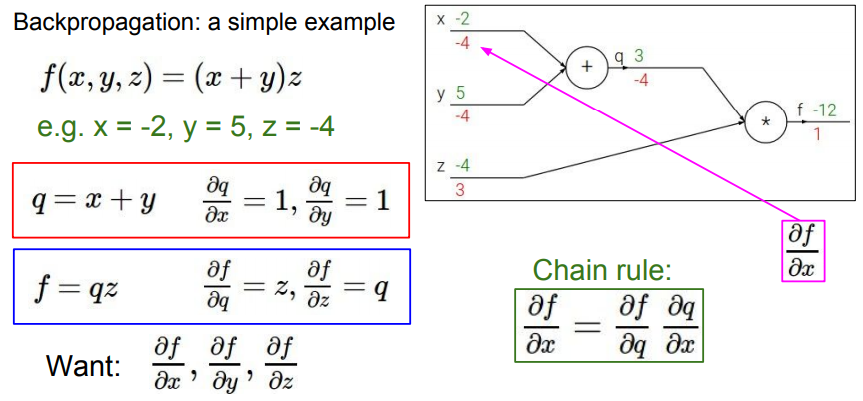
다음은 x, y, z가 f에 미치는 영향을 알아내기 위해 계산해 나가는 과정입니다.
1. 재귀적으로 계산해 나갑니다. 우선 q와 z를 구합니다.
q의 영향력 : df/dq는 -12/3으로 -4가 됩니다.
z의 영향력 : df/dz는 -12/-4로 3이 됩니다.
*곱 연산 시 노드별 미분값은 이전 노드의 변화량(미분값)*서로의 노드 값이 된다
2. x와 y는 바로 구할 수 없습니다. 따라서 위의 chain rule을 사용합니다.
x의 영향력 : df/dx는 df/dq*dq/dx로 df/dq*1입니다. 따라서 -4가 됩니다.
y의 영향력 : df/dy는 df/dq*dq/dy로 df/dq*1입니다. 따라서 -4가 됩니다.
*합연산시 노드별 미분값은 이전 노드 값이 된다
1. q = x + y에서 x로 편미분을 실시하면 dq/dx = dx/dx=1이 된다
2. df/dx = df/dq*1이 되므로, 이전 노드의 값이 된다
간단한 미분을 통해 각 노드가 score값에 미치는 영향력을 알아봤습니다. x는 -4, y는 -4, z는 3입니다. 이 각각의 값은 가중치를 update 할 때, 어떻게 업데이트해야 하는지 방향을 제시해줍니다.
위의 과정을 일반화해보면 다음과 같습니다(내용은 위의 예시와 동일하며, local gradient의 활용법에 집중하여 지켜봅시다). 순방향으로 계산해 나가서 z를 얻었습니다. local gradient값은 순방향으로 계산해 나가며 알 수 있으므로 이를 잘 기억해 둡니다. 이제 구해진 L(loss) 값을 가지고 역방향으로 계산해 나갑니다. 앞서 구해놓은 local gradient값과 global gradient(dL/dz)를 chain rule에 대입하여 gradient값을 계산해 나갈 수 있습니다.

위의 내용을 이해했다면 다음의 예제도 어렵지 않게 풀 수 있습니다(조금 복잡하긴 하지만요). gate별로 어떻게 대입해야 하는지는 아래 나와있으니 적절히 대입만 해주면 뚝딱입니다.

여기서 눈여겨보아야 할 점은 아래 그림의 파란색 네모 부분입니다. sigmoid function(활성화 함수)이라는 것을 활용하면 sigmoid gate라는 부분을 한 번에 계산할 수 있습니다(!!!).
*sigmoid gate와 같은 활성화 함수는 최종 값의 바로 앞에 위치해야 합니다.

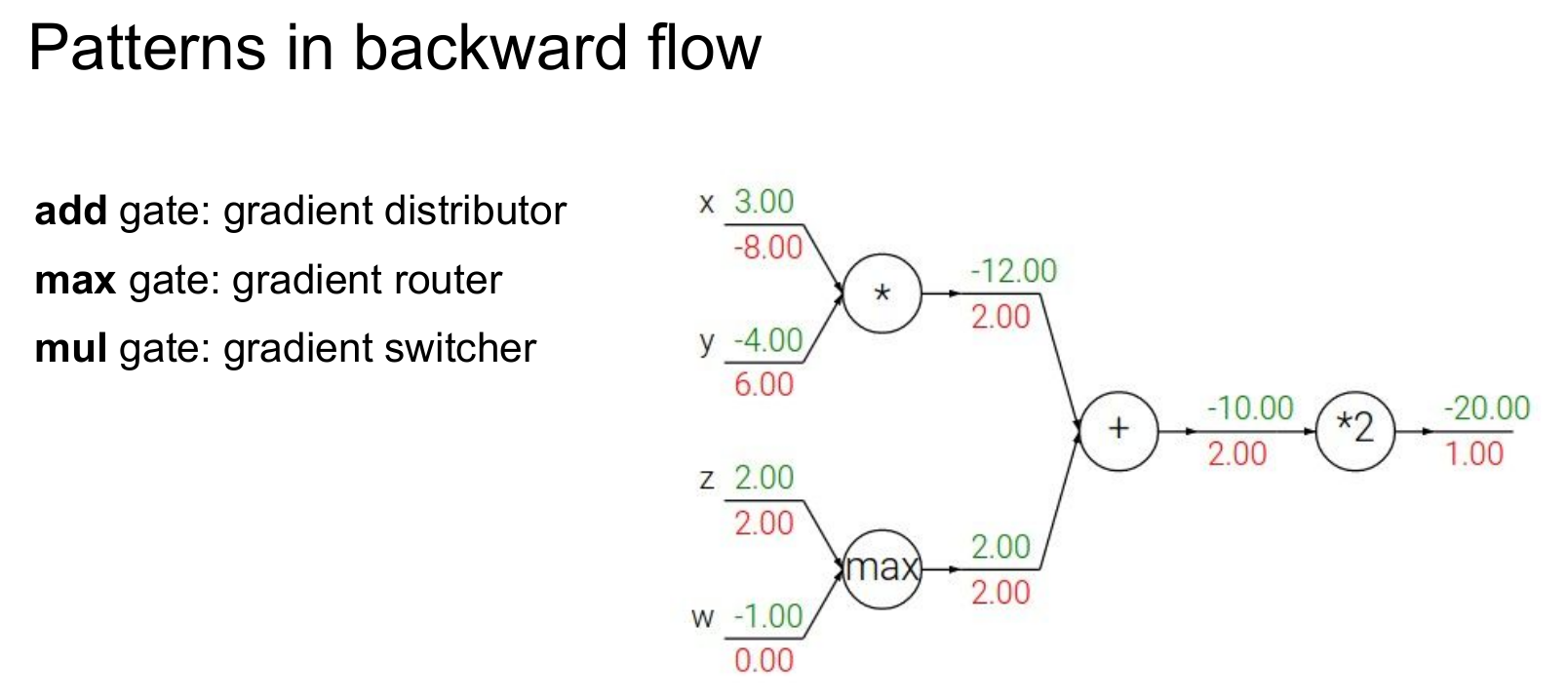
지금까지의 예제를 잘 헤쳐 나오셨다면, 위와 같은 몇 가지 특징을 눈치채셨을 수도 있습니다. 이를 잘 기억한다면 각 gate별로 굳이 계산을 하지 않아도 빠르게 미분값을 구할 수 있습니다.
add gate : 이전 노드의 미분값을 배분합니다.
max gate : 이전 노드의 미분값을 큰 쪽에만 넘겨줍니다(작은 쪽은 0).
mul gate : 이전 노드의 미분값을 현재 노드의 값과 곱해 교환합니다.
요약하자면
NN(Neural Network)은 일일이 계산하기엔 너무 거대합니다. 따라서 역전파를 사용합니다.
Back propagation(역전파)는 모든 gradient(기울기, 미분값)를 계산하기 위한 알고리즘입니다.
forward pass : 순방향으로 진행하며 gate별 결과를 계산하고 local gradient를 메모리에 저장합니다.
backward pass : loss function의 gradient를 계산하기 위해 chain rule을 적용합니다.
해당 글은 스탠퍼드 대학의 CS231n(Convolutional Neural Networks for Visual Recognition)을 정리한 글임을 밝힙니다.
'Note' 카테고리의 다른 글
| DEEPML(CS231n) Lec.06 Training Neural Networks, Part1 (0) | 2021.02.12 |
|---|---|
| DEEPML(CS231n) Lec.05 Convolutional Neural Networks (0) | 2021.01.31 |
| DEEPML(CS231n) Lec.04_1_1 What is backpropagation really doing? (0) | 2021.01.24 |
| DEEPML(CS231n) Lec.03_2 Optimization (0) | 2021.01.22 |
| DEEPML(CS231n) Lec.03_1 Loss Function (2) | 2021.01.10 |