지난 포스팅에서 Linear Classifier의 구조에 대해 공부했습니다. 우리의 목표는 Classifier가 제대로 된 분류를 통해 알맞은 라벨 값을 출력하는 거였죠. 그리고 이를 위해 가중치 W값이 어떤 역할을 하는지까지 알 수 있었습니다. 가중치는 Class별 각각의 픽셀 값을 가지고 새로운 이미지가 입력되었을 때, 해당 픽셀 값과의 곱 연산을 통해 나온 Prediction Score값을 통해 이미지의 라벨을 분류하는 역할을 하였습니다. 우리는 주어진 데이터 속에서 모델을 지속적으로 학습시키고 최적화시켜 나가야 합니다. 우리가 수정할 수 있는 것은 W값뿐이죠(입력 이미지와 출력 라벨은 정해져 있으니까요).
그렇다면 우리가 임의로 설정한 가중치가 어느 정도의 성능을 내고 있는 건지 궁금해집니다. 이때 이 가중치가 좋은지 나쁜지 눈으로 보고 판단하는 것은 좋은 방법이 아닙니다. 수치는 데이터에 따라 달라지기 때문이죠. 우리가 설정한 가중치가 얼마나 성능이 '구린지'를 판단할 수 있는 기준이 필요합니다. 이것이 바로 이번 강의의 핵심 Loss Function입니다.
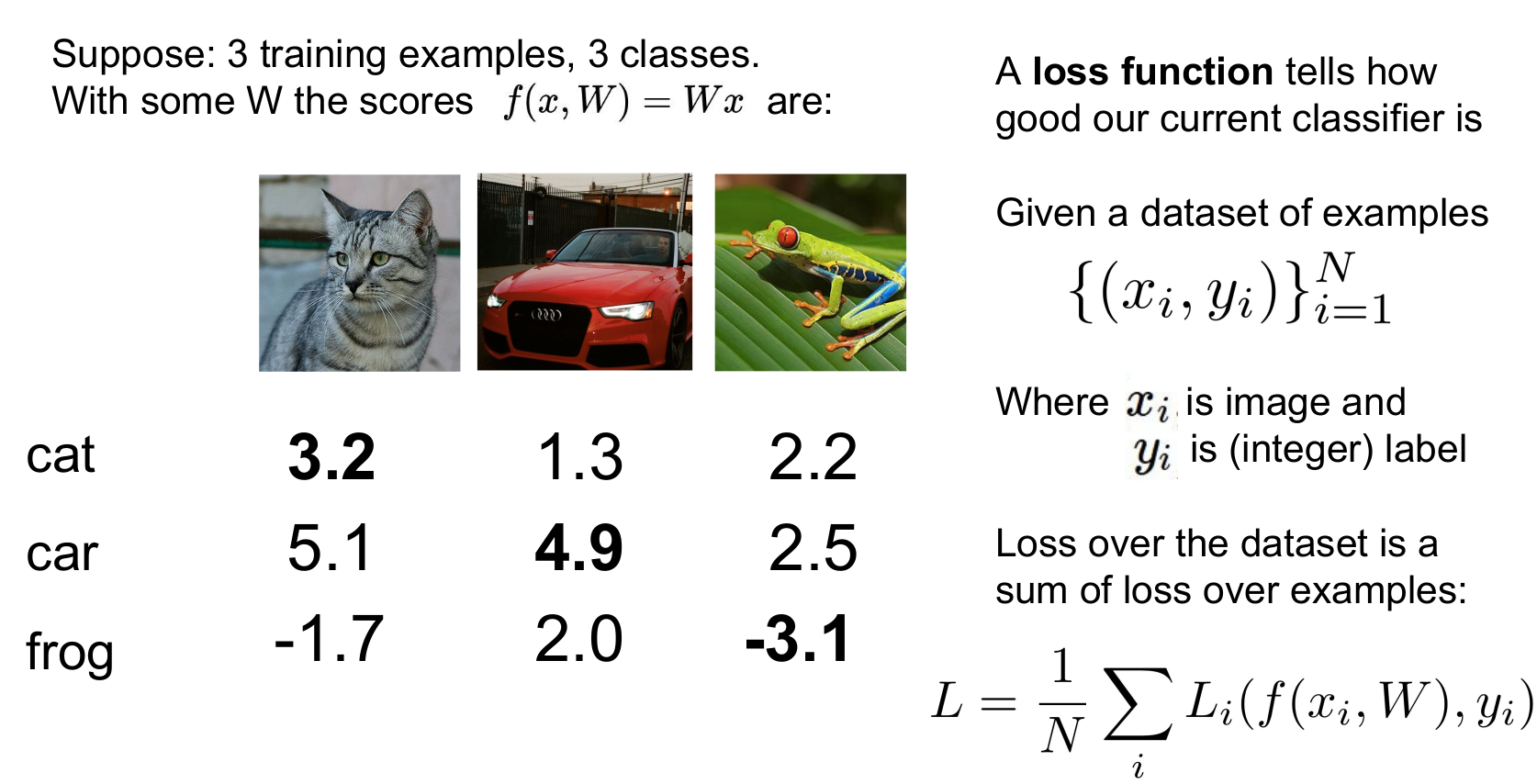
위 사진에서 우리는 3가지 Class에 대한 Prediction Score를 얻을 수 있습니다. 자동차는 제대로 분류했지만, 고양이 분류 성능은 그다지 좋지 못하고, 개구리는 가망이 없습니다. 이 과정을 공식화해보면 사진 1의 오른쪽과 같습니다. 이때 x는 주어진 이미지이고 y는 정답인 클래스의 라벨입니다(y[i]의 i정도 되려나요?). y는 10개의 클래스이므로 1~10, 또는 0~9의 정수 값을 갖습니다(프로그래밍 언어에 따라 다름).
손실 함수 L_i는 예측 함수 f와 정답 값 Y를 입력으로 받아서 이 트레이닝 샘플을 얼마나 '구리게' 예측하는지를 정량화시켜줍니다. 우리가 원하는 것은 전체 데이터셋, 그리고 전체 클래스를 일반화할 수 있는 Loss Function을 구하는 것이기 때문에 전체 트레이닝 셋을 N으로 나눠줍니다. 최종 Loss인 L은 우리 데이터셋에서 각 N개의 샘플들의 Loss평균이 됩니다.
Multiclass SVM Loss

보다 구체적으로 살펴보겠습니다. 그림 오른쪽은 이미지 분류에 활용하기 좋은 Multiclass SVM loss입니다. 이는 이진 분류기법인 SVM을 여러 클래스를 다루기 위해 일반화한 형태입니다. 일반적으로 다음과 같은 과정을 거칩니다.
각 트레이닝 데이터로부터 Loss L_i 구하기
1. 올바른 카테고리와 올바르지 않은 카테고리의 스코어 비교
2. True인 카테고리를 제외한 나머지 카테고리 Y를 연산(C-1회)
3. Syi > Sj & 격차가 일정 마진 이상이라면(여기선 1)
True = 의미있게 크다(Loss가 0이 된다)
False = 클래스 내의 연산한 수치를 모두 더한 값이 loss가 된다
*이때 Syi는 정답인 클래스의 스코어, Sj는 정답이 아닌 클래스의 스코어

우측 상단 그래프는 "Hinge loss"라고 합니다. X축은 S_yi(정답 클래스 스코어), Y축은 Sj(손실)의 형태를 보여줍니다. 해석은 간단합니다. 정답 카테고리의 점수가 올라갈수록, loss는 선형적으로 줄어듭니다. 이 loss는 0이 된 후에도 safety margin을 넘어설 때까지 계속해서 줄어듭니다. (이때 margin이 몇인지는 크게 중요하지 않습니다. 결국 알고 싶은 건 Loss Function의 정확한 score가 아닌 스코어 간의 '상대적인 차이'이기 때문이죠. margin값은 scailing 하면 결국 상쇄되어 사라집니다.)
S는 분류기의 출력으로 나온 예측된 스코어
y_i는 이미지의 실제 정답 카테고리(정수 값)
위 사진에서 고양이는 S_1, 자동차는 S_2, 개구리는 S_3
∴ S_y_i는 한 이미지의 결과값 중 정답 클래스의 스코어

손실 함수의 계산은 [정답이 아닌 클래스 - 정답 클래스 + safety margin]의 구조를 갖습니다. 실제로 계산해보면 보다 쉽게 이해할 수 있습니다. 우선 정답이 아닌 클래스를 순환합니다. cat을 먼저 살펴봅시다. cat → car는 5.1 - 3.2 +1로 2.9의 loss값이 나타납니다. cat → frog는 - 1.7 - 3.2 +1로 -3.9의 값을 갖습니다. loss값이 0보다 작은 경우 0이 되므로 cat class의 최종 loss값은 2.9가 됩니다.

연습 삼아 자동차도 계산해 보겠습니다. car → cat의 loss값은 1.3 - 4.9 + 1 = - 2.6이며, car → frog의 loss값은 2.0 - 4.9 + 1 = - 1.9로 car의 최종 loss값은 0입니다. frog는 12.9의 loss값을 갖습니다.
전체 데이터 셋에서 이러한 과정을 거친 최종 Loss는 각 트레이닝 이미지의 Loss의 평균이 될 것입니다. 이 예시에선 (2.9 + 0 + 12.9) / 3으로 우리의 분류기는 현재 5.3만큼 '구리게' 분류하고 있다는 정량적 지표가 됩니다.
SVM Loss Function의 성질
1. 스코어 값의 성질

우리는 Loss Function이 실제로 어떤 방식으로 작용하는지 직관적으로 이해하기 위해 위와 같은 질문을 생각해 볼 수 있습니다. 다른 클래스에 비해 월등히 크기 때문에 car score를 조금만 바꾸는 것은 Loss에 큰 영향을 미치지 않는다는 것을 알 수 있습니다. SVM loss는 정답 스코어와 그 외 스코어 간의 차이만 고려하기 때문이죠(어차피 0이 나옵니다).
2. Loss Function의 최대, 최소
Loss Function의 최대, 최솟값은 얼마일까요? 최댓값은 무한대, 최솟값은 0이 나올 것입니다. 앞에 나온 Hinge Loss를 다시 볼까요? x축은 정답 클래스 score, y축은 loss라고 했습니다. 최댓값은 정답 클래스 스코어가 작을수록 크게 나타날 것이며, 이는 무한대로 뻗어나갑니다. 최솟값은 모든 클래스에서 정답 클래스 score가 가장 높은 경우 0까지 떨어질 수 있습니다.

3. Loss Function의 디버깅

파라미터를 초기화시키고 처음부터 학습시킬 때, 일반적으로 행렬 W를 임의의 작은 수로 초기화시킵니다. 이때 초기 학습단계에서 결과 스코어가 임의의 일정한 값을 갖습니다. 그렇다면 만약 모든 스코어 S가 거의 "0에 가깝고 값이 서로 비슷하다면", Multiclass SVM에서 Loss는 어떻게 될까요?
말이 어렵습니다. 위 사진을 예시로 들어볼게요. 만약 고양이의 score를 알고 싶은데 세 score가 매우 작은 값을 갖는 다른 수라고 생각해볼게요. 연산은 [정답이 아닌 클래스 - 정답인 클래스 + safety margin]을 C-1번(정답인 클래스는 제외하니까요) 순환하죠.
예를 들면 cat = 0.00097, car = 0.00098, frog = 0.00099입니다. cat의 score가 알고 싶으면 두 번의 연산을 해야 하죠? 0.00098 - 0.00097 + 1 = 1.00001, 0.00099 - 0.00097 + 1 = 1.00002입니다. 이러면 loss값은 2.00003이 되겠군요. 이때 loss값은 2와 매우 작지만 0은 아닌 수들의 합으로 나타납니다. 따라서 loss값은 "Class의 수 - 1"의 값으로 나타납니다.
이는 "디버깅 전략"으로 매우 유용한 성질입니다. 만약 이러한 성질을 염두에 두고 트레이닝을 시작한다면, 첫 Loss값을 짐작해 볼 수 있죠. 다시 말해 첫 트레이닝의 Loss 결과물이 C-1이 아니라면, 아마 다시 시작하셔야 할 것입니다.
4. C-1회 순환하는 이유

그러면 정답인 클래스까지 다 더한다면 어떤 일이 일어날까요? 결론부터 말하자면 모든 Loss에서 1이 증가할 것입니다. 사실 Loss에 모든 클래스를 다 더한다고 분류기가 달라지는 것은 아닙니다. 그러나 우리는 정답인 클래스를 계산에 포함시키지 않음으로써 Loss가 0인 결과물을 "잃은 것이 없는 상태"라고 직관적으로 이해할 수 있습니다.
5. Loss 계산 시 SUM 대신 MEAN을 활용한다면?

클래스의 개수는 어차피 정해져 있으니 평균을 취하는 것은 단지 함수를 리스케일할 뿐입니다. 따라서 결과는 변하지 않으며 단지 스케일만 변할 것입니다. 사실 스코어 값이 중요한 문제라면 리스케일 시 결과에 변화가 생기겠지만 이 역시 스코어 값이 아닌 상대적인 크기에만 관심이 있는 Loss Function의 성질 때문에 영향을 받지 않습니다.
6. Loss Function에 제곱을 해준다면?

결과는 달라집니다. 제곱을 해주는 건 잘 예측한 것과 잘못 예측한 것 사이의 트레이드오프를 비 선형적인 방식으로 바꿔주는 것입니다. 이렇게 되면 손실 함수의 계산 자체가 바뀌게 됩니다. 실제로 squared hinge loss를 종종 사용하는데, 목적에 따라서 손실 함수를 설계할 때 사용할 수 있는 한 가지 선택지가 될 수 있습니다.
그렇다면 어떤 경우일 때 이러한 방식을 취해주는 걸까요? 우리가 손실 함수를 구하는 목적은 현재 가중치가 얼마나 별로인지를 정량화하는 것입니다. 만약 설계자가 다양한 방식으로 실수를 저지르고 있다면, 어떻게 해야 이 분류기가 만드는 다양한 Loss들 마다 상대적으로 페널티를 부여할 수 있을까요? 제곱을 하는 행위는 이런 경우 의미 있어집니다. 우리는 Hinge loss에서 '얼마나 잘못되었는지'에 대한 고민은 하지 않았습니다. 상대적인 크고 작음만이 고려의 대상이었죠. 그러나 제곱을 할 경우 잘못된 것은 훠어어얼씬 잘못되어지고 우리는 '무엇'이 '왜' 잘못되었는지를 고려해야 할 때 사용할 수 있습니다.
결국 우리가 에러에 대해 얼마나 신경 쓰고, 어떻게 정량화할 것인지에 달렸습니다. 이는 실제로 알고리즘을 설계할 때 어떤 에러를 신경 쓰고 있는지, 그리고 어떤 에러가 트레이드오프 되는 것인지 알려주는 것은 매우 중요(super important)합니다.
7. W가 0인 모델을 찾았다고 할 때, 이 W의 값은 유일할까?

우리가 W값이 0이 되는 지점을 찾았다고 할 때, W값은 유일하지 않습니다. 지속적으로 나오는 Loss function의 성질이 있습니다. 정답 클래스의 prediction score 값이 다른 클래스와 비교해서 유의미하게 크다면, 우리는 크기의 차이는 신경 쓰지 않습니다. 단지 크기만 신경 쓸 뿐이죠. 이 문제도 마찬가지입니다. 자동차의 경우 W값에 2배를 해준다면(더블 더블유가 되므로, 쿼드유랍니다 여러분), prediction score의 값도 2배가 될 것입니다. 그러나 결과에는 변함이 없죠. 아래의 사진과 같습니다.

Regularization
여기서 한 가지 의문이 생깁니다. 전체 loss값이 0이 된다는 건 하나도 틀리지 않고 제대로 예측했다는 얘기인데... 뭔가 찝찝합니다. 우리가 만약 갖은 노력 끝에 loss값에 집착해서 모든 loss가 0이 되는 W값을 찾았다고 한다면, 과연 좋은 결과물이라고 말할 수 있을까요? 지금의 의문은 다음과 같이 나타낼 수 있습니다.

만약 train data에서 모든 데이터의 loss가 0이 되는 지점을 찾는다면 우리의 모델은 모든 파란 점을 완벽하게 잇는 파란선이 될 것입니다. 그러나 이 상황에서 새로운 데이터가 들어온다면, 파란 선으로는 이를 제대로 분류할 수 없습니다. 사실 우리의 목적은 새로운 데이터를 분류할 수 있는 분류기를 찾는 것인데 말이죠. 우리가 할 수 있는 건 오직 트레이닝 데이터에 핏 해라!! 뿐이니 두 손 놓고 지켜볼 수밖에 없는 걸까요?
우리는 이 문제를 해결할 수 있는 방법을 Regularization이라고 합니다. 'Data Loss Term'에서는 분류기가 트레이닝 데이터에 핏하게 하고 여기에 손실 함수에 Regularization Term()을 추가하는데, 이것이 모델이 좀 더 단순한 모델(데이터나 모델에 따라 다름)을 선택하도록 도와줍니다. 일반적으로 비슷한 설명력을 갖는다면, 보다 단순한 모델을 설정해야 합니다. 이것이 보다 미래를 잘 예측할 수 있기 때문입니다.
예를 들어 다음과 같은 가설들이 있다고 가정합시다.
보름달이 뜬 밤 범죄율이 높다
기온이 35도인 날 범죄율이 높다
12월 31일 범죄율이 높다
이 세 가지 가설이 실제로 범죄율을 잘 설명한다고 할 때, 세 가지를 완벽하게 만족하는 날을 찾아 범죄 단속에 나가는 것보다 12월 31일 범죄 단속을 하는 것이 더 일반적인 상황을 예측할 수 있을 것입니다(12월 31일에 보름달이 뜨고 기온이 35도인 날이 있을까요?).
기계학습에선 이러한 직관을 적용하기 위해 Regularization Penalty라는 것을 추가해줍니다. 이를 통해 모델이 train data에 더 fit 해지려(복잡해지려) 할 때 penalty를 주는 방법입니다. 이 경우 손실 함수는 항을 두 개 갖습니다(Data loss, Regularization loss). 그리고 Regularization의 하이퍼 파라미터 람다, 두 항 간의 트레이드오프)가 추가됩니다
*트레이드오프 : 한쪽이 증가하면 한쪽은 감소하는 관계

위의 사례들은 모두 기계학습과 딥러닝에 사용되는 Regularization 방식입니다. 간단히 정리해 보자면 다음과 같습니다.
- L1 Regularization(L1 norm), W(L1)에 페널티를 부과 → 행렬 W가 희소 행렬이 되게 함
- L2 Regularization(L2 norm), W(L2)에 패널티를 부과
- Elastic net regularization : L1 + L2(함께 사용)
- Max norm regularization : L1, L2 norm 대신 max norm을 사용
- 딥러닝 특화 : Dropout, Batch normalization, Stochastic depth
가장 보편적인 것은 L2 Regularization(Weight decay)입니다. L2 Regularization은 W에 대한 Euclidean Norm(L2 norm, Squared Norm)입니다. 가중치 행렬 W의 euclidean norm에 페널티를 주는 방식으로 동작합니다. *Norm : 두 벡터 사이의 거리를 측정하는 방법(또는 함수)
모델이 복잡한 방향으로 학습할 때 Regularization을 실시한다고 했습니다. 그렇다면 모델이 복잡한지 아닌지 판단하는 기준은 뭘까요?
L1 Regularization과 L2 Regularization의 차이

위와 같은 예시가 있습니다. 예시에는 우리의 이미지 데이터 x와 두 가중치가 있습니다. Linear classification의 관점에서 두 가중치는 같습니다. 결과적으로 두 가중치는 같은 score값을 산출하기 때문이죠(score = 1). 그러나 Regularization마다 선호하는 가중치의 구성이 다릅니다.
L1 Regularization은 w1을 선호합니다. L1 Regularization은 가중치 W의 0의 개수에 따라 모델의 복잡도를 다룹니다. 0이 적으면 차이가 명확하지 않은 복잡한 모델이라고 인지합니다. 일반적으로 Sparse한(0이 많은) Solution을 선호하는 것이죠.
반면 L2 Regularization은 w2를 선호할 것입니다. w2가 norm이 더 작게 나타나기 때문입니다. L2 Regularization은 분류기의 복잡도의 기준을 더 coarse(지저분) 한 것으로 둡니다. 값이 매끄러운(편차가 적은) W를 선호하는 것이죠. 특정한 값이 라벨을 결정하는 것이 아닌 x의 모든 요소가 영향을 주는 것을 선호합니다.
따라서 모델이 복잡도를 어떻게 정의하는가, 그리고 복잡도를 어떻게 측정하느냐 라는 질문은 '우리가 처한 문제 또는 데이터에 따라 다르다'라고 할 수 있습니다. 따라서 모델 설계 시 열심히 고려해야 합니다.
Softmax loss(Multinominal logistic regression)
다음은 Softmax loss에 대해 생각해보겠습니다. 사실 딥러닝에선 앞의 SVM loss보다 Softmax loss가 더 많이 사용됩니다. 여기선 Score값의 크기가 의미 있어집니다. '확률'로 나타낼 거거든요. Softmax loss의 과정을 요약하자면 다음과 같이 간단히 나타낼 수 있습니다. Softmax 함수를 이용하여 자연상수 e(약 2.7)를 스코어값만큼 제곱해주고(양수), 여기에 -log(얼마나 '구린지'를 알고 싶기 때문에)를 취해주는 것입니다( = -log(P(정답클래스))). 이 과정을 고양이(our favorite, beautiful cat)의 이미지로 설명해 보겠습니다.

우리는 Linear Classifier를 활용해 Class별 score를 구했습니다. 이번엔 스코어 자체를 Loss로 쓰지 않습니다. 우선 이 score를 지수화(exponentiate)합니다. 그리고 합이 1이 되도록 정규화(normalize) 합니다. 그리고 도출된 정답클래스 스코어의 확률값에'만' -log를 씌워줍니다.
위에서 우리는 몇가지 물음으로 SVM Loss에 대해 이해할 수 있었습니다. 이번에도 몇 가지 같은 질문을 통해 Softmax Loss의 성질에 대해 알아봅시다.
Softmax Loss Function 스코어 값의 성질
1. Loss Function의 최대, 최소
Softmax Loss의 최댓값은 무한대이며 최솟값은 0입니다. 확률이란 관점에서, 우리의 확률값은 0에서 1까지 분포하고 있습니다. log안에 들어갈 어떤 수는 1이 되어야 한다는 얘기입니다. 정답 클래스에 대한 log확률이기 때문에 log(1) = 0이고, -log(1) 또한 0입니다. 그러므로 완벽하게 고양이를 분류한 Classifier의 경우, loss는 0이 될 것입니다.
그렇다면 loss가 0이 되게 하는 실제 스코어 값은 어떤 값이어야 할까요? 위 그림에서 간단하게 생각해봅시다. 초록색 네모의 probability 부분을 보시면, 지수화를 하기 때문에 상대적으로 큰 car의 값이 0.06이 나온 반면 cat의 경우 0.89의 큰 값이 나왔습니다. 이를 비추어보면 만약 정답 score값이 무한하게 커진다면, 그래서 극단적으로 높아진다면 P(score)의 값은 1에 가까워져서 loss값은 0에 가까워질 것입니다. (그러나 컴퓨터는 무한대 계산을 잘 못하기 때문에 loss가 0인 경우는 없음, 유한정밀도)
2. Loss Function의 디버깅
만약 모든 스코어 S가 거의 "0에 가깝고 값이 서로 비슷하다면", Multiclass SVM에서 Loss는 어떻게 될까요? log(c) = -log(1/c)로 나타나며 만약 log(c)가 아니라면 다시 생각해 봐야 합니다.
SVM vs. Softmax

이번 강의를 한번 정리해봅시다. Linear Classifier가 하는 일은 동일합니다. 이미지를 학습하고, 가중치 행렬을 찾고, 입력받은 이미지에 곱연산을 거쳐(bias도 더해줍니다 ) class별 predict score를 구합니다.
이후 각각의 loss function을 통해 loss값을 구하고, R(W)를 더해서 최종 loss값을 도출합니다. 여기서 둘의 차이점이 나타납니다. 우리가 설정한 가중치가 '얼마나 구린지'(이것보다 좋은 표현이...갓초월번역)를 측정하기 위해 loss score를 해석할 때, SVM은 정답 스코어와 정답이 아닌 스코어 간의 margin을 신경 썼습니다. 반면 Softmax는 확률을 구해서 -log(P(정답 클래스))를 신경 씁니다.
이런 두 방식의 차이 때문에 개선 노력에도 차이가 나타납니다. SVM의 경우 일정 선(margins)을 넘으면 그 순간 성능 개선을 멈춥니다. 그러나 Softmax의 경우 지속적으로 확률을 높이기 위해 노력합니다. 실제 딥러닝 학습 시 성능에 큰 차이가 나타나진 않지만, 성질을 알고 있는 것은 도움이 됩니다)
y_i [0] 일 때,
x = [100, 99, 98, 97]라면 SVM의 loss는 0이 나오고 개선을 멈춥니다.
Softmax는 [10000, 30, 1, 1]이어도 끊임없이 값을 무한대에 가깝게 올리려고 노력합니다.
이렇게 길게 늘여쓴 오늘의 강의는 사실 아래 사진 한 장으로 요약이 가능합니다.

딥러닝은 간단합니다.
엄청나게 복잡한함수 f(x)를 정의하고- 파라미터 값이 주어졌을 때 알고리즘이 얼마나 '구리게' 작동하는지 측정할 손실 함수를 작성하고
- 모델이 복잡해지는 것을 막을 수 있는 Regularization term을 추가합니다.
- 그리고 이 모든 것을 합쳐서 최종 손실 함수가 최소가 되게 하는 가중치 행렬이자 파라미터인 행렬 W를 구하는 것입니다.
- 이번 강의에서는 이중 2. 의 손실 함수를 구하기 위해 활용할 수 있는 Loss function으로 두 가지를 배웠습니다.
요약하자면
SVM은 스코어 자체에 대한 해석은 하지 않고 단지 정답클래스가 다른 클래스에 비해 높은 점수를 내는지만 관심 있습니다. 스코어가 의미하는 건 고려하지 않았습니다.
softmax는 스코어 자체에 추가적인 의미를 부여합니다. 스코어를 특정 수식에 대입해 클래스별 확률 분포까지 계산합니다.
해당 글은 스탠퍼드 대학의 CS231n(Convolutional Neural Networks for Visual Recognition)을 정리한 글임을 밝힙니다.
'Note' 카테고리의 다른 글
| DEEPML(CS231n) Lec.04_1 Backpropagation (0) | 2021.01.25 |
|---|---|
| DEEPML(CS231n) Lec.04_1_1 What is backpropagation really doing? (0) | 2021.01.24 |
| DEEPML(CS231n) Lec.03_2 Optimization (0) | 2021.01.22 |
| DEEPML(CS231n) Lec.02_2 Linear Classification (0) | 2021.01.04 |
| DEEPML(CS231n) Lec.02_1 Image Classification (10) | 2020.12.31 |