이번 강의에선 크게 세 가지를 다룹니다.
1. One time setup
- activation functions, preprocessing, weight initialization, regularization, gredient checking
2. Training dynamics
- babysitting the learning process, parameter updates, hyperparameter optimization
3. Evaluation
- model ensembles
1. Activation Functions
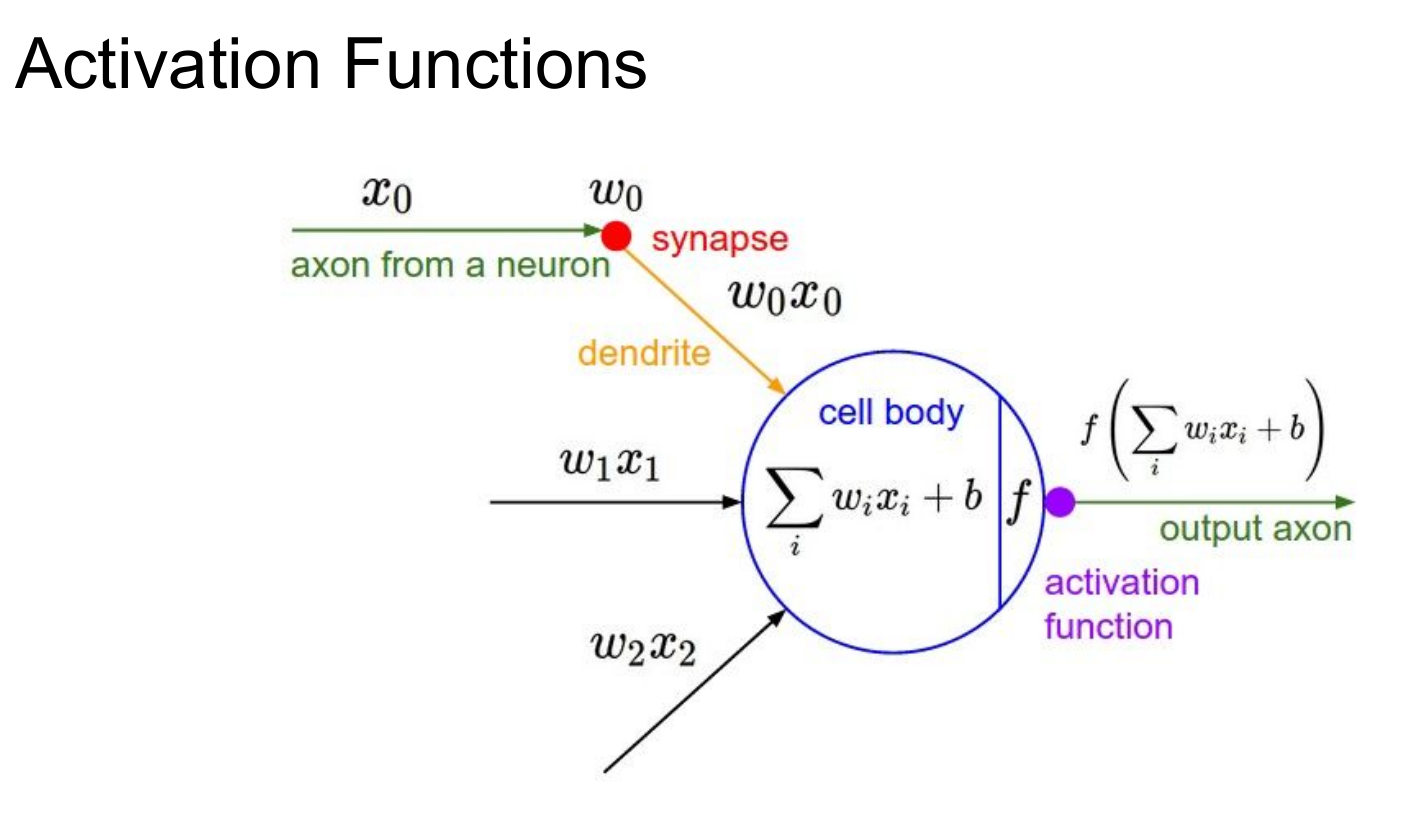
인간의 신경망과 비교하면 위와 같은 단계를 거치게 됩니다. 이전 뉴런의 정보(x1)를 다음 뉴런으로 전달하는 역할을 하는 시냅스(w0)를 거쳐 cell body에 저장됩니다. 이 결과를 또 다음 cell body에 전달해야 하는데, 이때 사용하는 함수 f(x)를 활성화 함수(activation function)라고 합니다. 일반적으로 활성화함수는 *비선형함수를 사용합니다.
*선형함수는 쌓아도 선형으로 돌아가기 때문(층이 쌓이지 않는다)
우리는 활성화 함수의 종류를 살펴보고, 각 함수의 특징과 단점을 살펴볼 것입니다. 일반적인 활성화 함수의 종류는 다음과 같습니다.
*특징과 단점의 비교를 위한 문장단위 구성 주의

1-1. Sigmoid
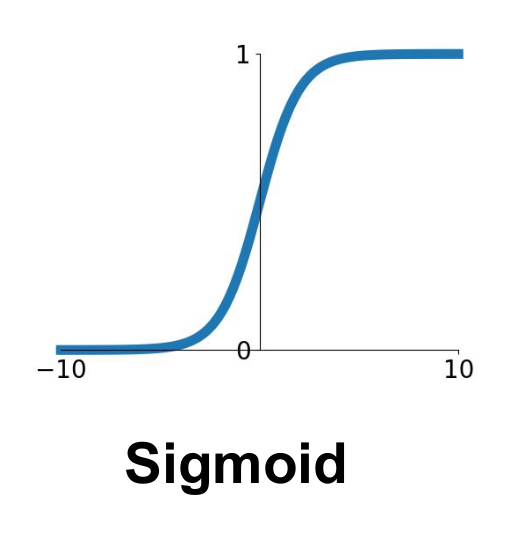
특징
가장 전통적인 방법
이진분류에서 많이 사용(이마저도 최종출력에서만 사용)
기울기가 큰 0.3~0.7 구간에서 잘 작동함
단점
기울기 소실(Saturated neurons “kill” the gradients, gradient vanishing)
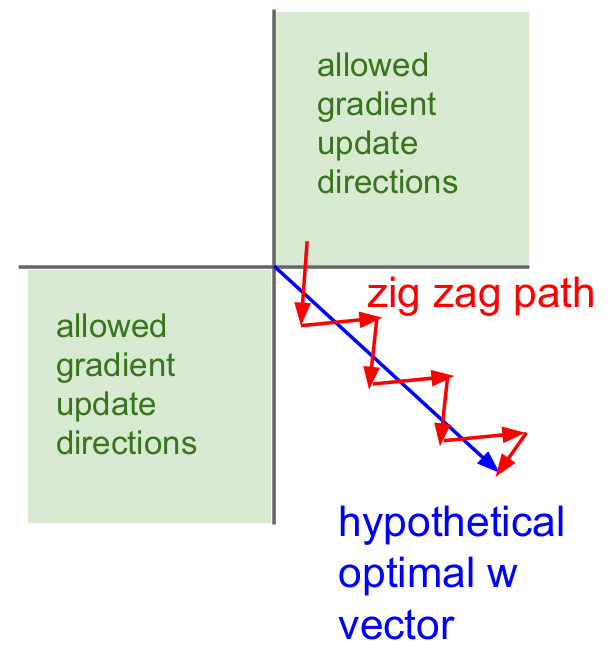
Sigmoid outputs are not zero-centered(Always all positive or all negative, zig zag path)
exp() is a bit compute expensive
1-2. tanh(x)

특징
Squashes numbers to range [-1,1]
zero centered (nice)
단점
still kills gradients when saturated :(
1-3. ReLU


특징
Computes f(x) = max(0,x)
Does not saturate (in +region)
Very computationally efficient
Converges much faster than sigmoid/tanh in practice (e.g. 6x)
Actually more biologically plausible than sigmoid
(Rectified Linear Unit)
가장 많이쓰는 활성화함수
단점
Not zero-centered output
An annoyance
- x < 0일 때 가중치가 업데이트 되지 않음(일반적으로 10~20%)
- 초기 가중치 설정(초기값이 너무 크면 데이터로부터 떨어져 가중치 업데이트가 안됨)
- learning rate가 높을 때(초기엔 잘 학습되다가 업데이트 안됨)
1-4. Leaky ReLU
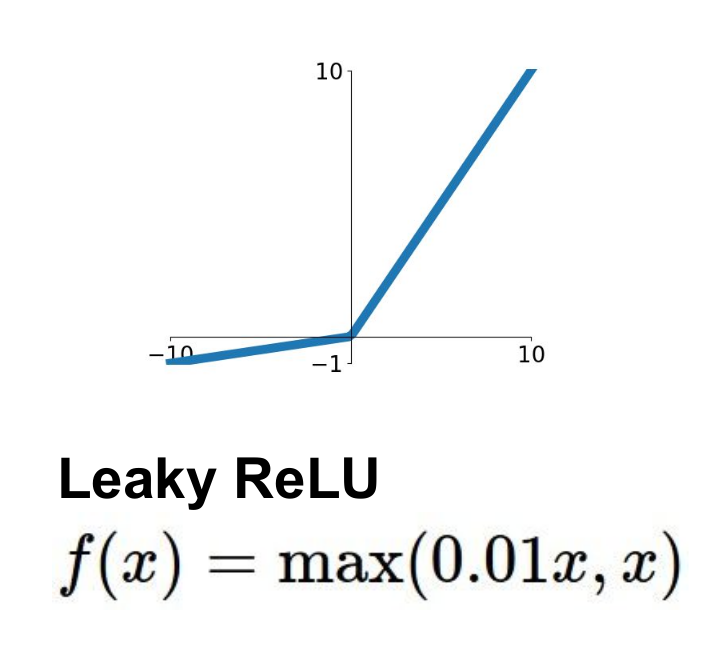
특징
Does not saturate
Computationally efficient
Converges much faster than sigmoid/tanh in practice! (e.g. 6x)
will not “die”.
1-5. ELU
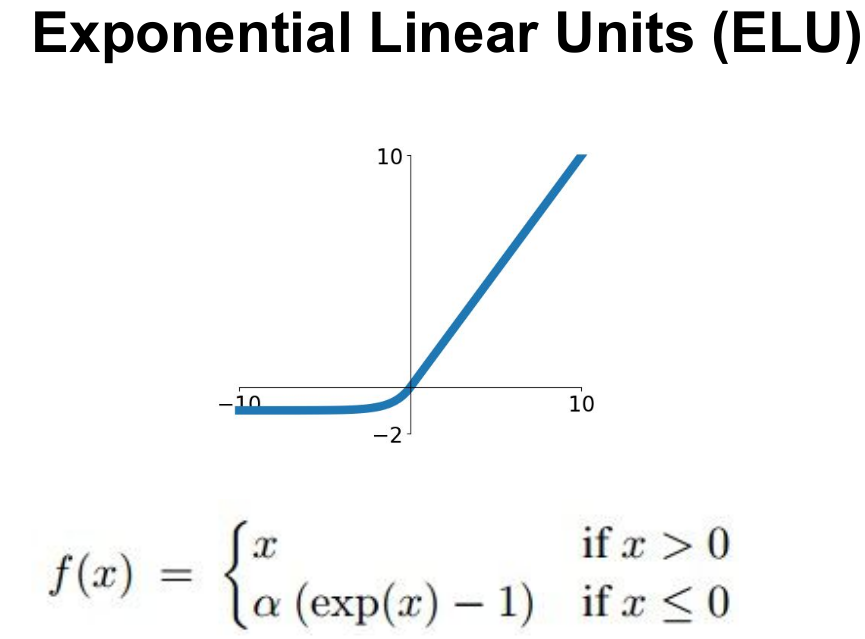
특징
All benefits of ReLU
Closer to zero mean outputs
Negative saturation regime
compared with Leaky ReLU
adds some robustness to noise
단점
Computation requires exp()
1-6. Maxout "Neuron"
특징
Does not have the basic form of dot product -> nonlinearity
Generalizes ReLU and Leaky ReLU
Linear Regime! Does not saturate! Does not die!
단점
doubles the number of parameters/neuron(메모리가 두배로 소모됨)
요약
ReLU를 씁시다
*learning rate, W 초기값 설정만 주의
다른 함수를 시도정도'는' 해볼 수 있습니다.
시그모이드는 쓰지 맙시다
2. Data Preprocessing

우리에게 주어진 데이터 뭉치가 있을 때, 이를 좌표 평면 위에 나타낼 수 있습니다. 보다 정확한 분석을 위해 데이터 전처리를 해줘야 합니다. 데이터 전처리에는 일반적으로 다음과 같은 3가지 방법을 사용합니다.
1. 우리는 위에서 데이터가 zero-centered하지 못하면 zig-zag path 문제가 생기는 것을 보았습니다. 이를 방지하기 위해 각 점에서 평균을 차감해주는 방법을 사용합니다. 기하의 관점에서 보면, 모든 점을 원점으로 모아주는 역할을 합니다.
2. 다음으로 데이터를 정규화 해줍니다. 이는 다양한 데이터를 동등한 수준으로 분석할 수 있게 해줍니다.
데이터 정규화와 표준화는 항상 헷갈리는 개념입니다. 한번 짚고 넘어가겠습니다. 둘 모두 데이터의 학습이 원할하게 진행되는 것을 돕기 위해(scale이 큰 feature의 영향력 과대를 방지하기 위해) 실시합니다. local minima에 빠질 위험이 감소하고 연산이 빠르게 진행되는 특징이 있습니다.
표준화(Standardization)
데이터의 진폭 감소(평균이 0, 분산이 1)
데이터의 간격이 감소하게 됨(0과 1을 벗어날 수 있음)
데이터가 평균으로 부터 얼마나 떨어져있는지를 보여줌
정규화(Normalization)
데이터를 0과 1 사이의 값으로 변환(Scaling)
최댓값은 1, 최솟값은 0을 벗어날 수 없음
데이터군 내에서 특정 데이터의 위치를 보여줌

3. PCA나 Whitening기법도 있습니다. PCA는 차원을 축소하는 역할을 하며, Whitening은 기존의 데이터가 가지고있던 상관성과 강도를 제거하여 아무 정보가 없는 데이터 분포로 만들어줍니다.
3. Weight Initialization
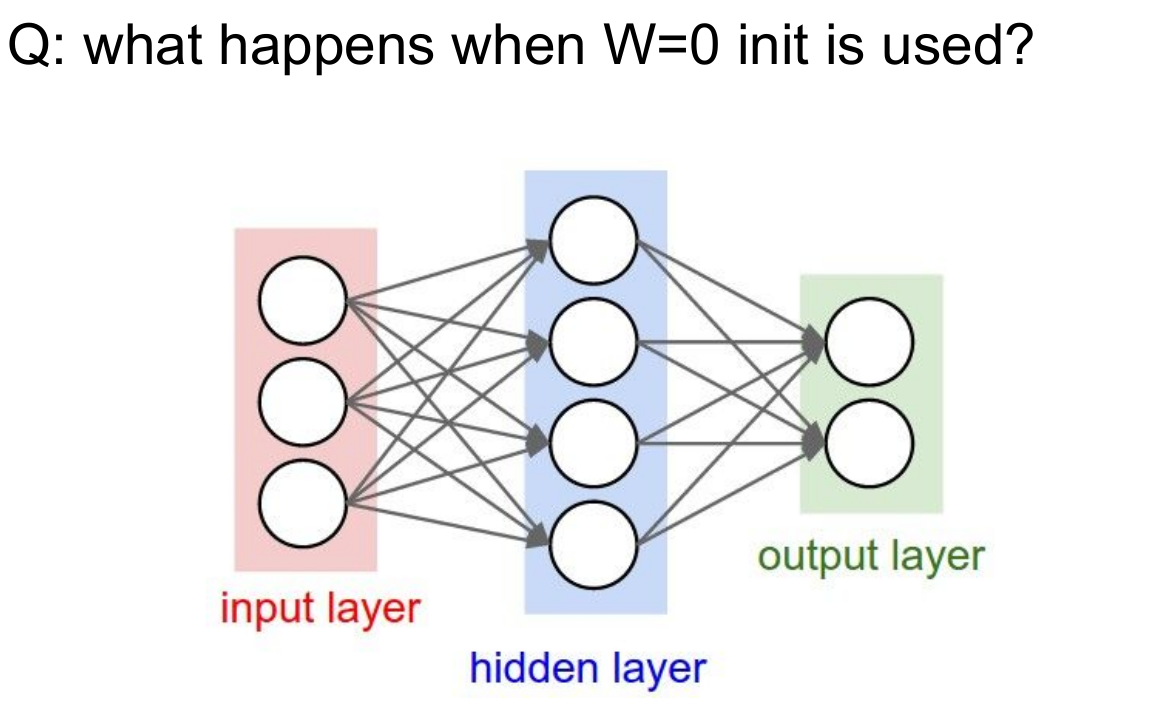
초기 모델을 구상할 때 가중치를 어떻게 설정하는 것이 좋을까요? 물론 정방향, 역방향으로 반복 진행하며 가중치를 지속적으로 업데이트 할 것이지만, 초기 가중치를 설정하는 것 역시 중요합니다. 예를 들어 초기 가중치값을 0으로 설정한다면, '모든 뉴런이 같은 일'을 하게 됩니다. 모두 같은 W값을 사용하기 때문에 같은 출력값이 도출되고 이를 바탕으로 하는 가중치 업데이트 역시 진행되지 않습니다. 그렇다면 가중치는 어떤 수치로 초기화해야 할까요? 극단적이긴 하지만 다음 두 사례를 보면 감을 잡을 수 있습니다.
3-1. Initialization too small
우선 매우 작은 수치로 초기화하는 경우입니다. 일반적으로 가중치는 0이 아닌 임의의 작은 수로 초기화합니다. 0을 평균으로 하고 표준편차가 0.01인 가우시안 분포에서 초기값을 추출해봅시다.
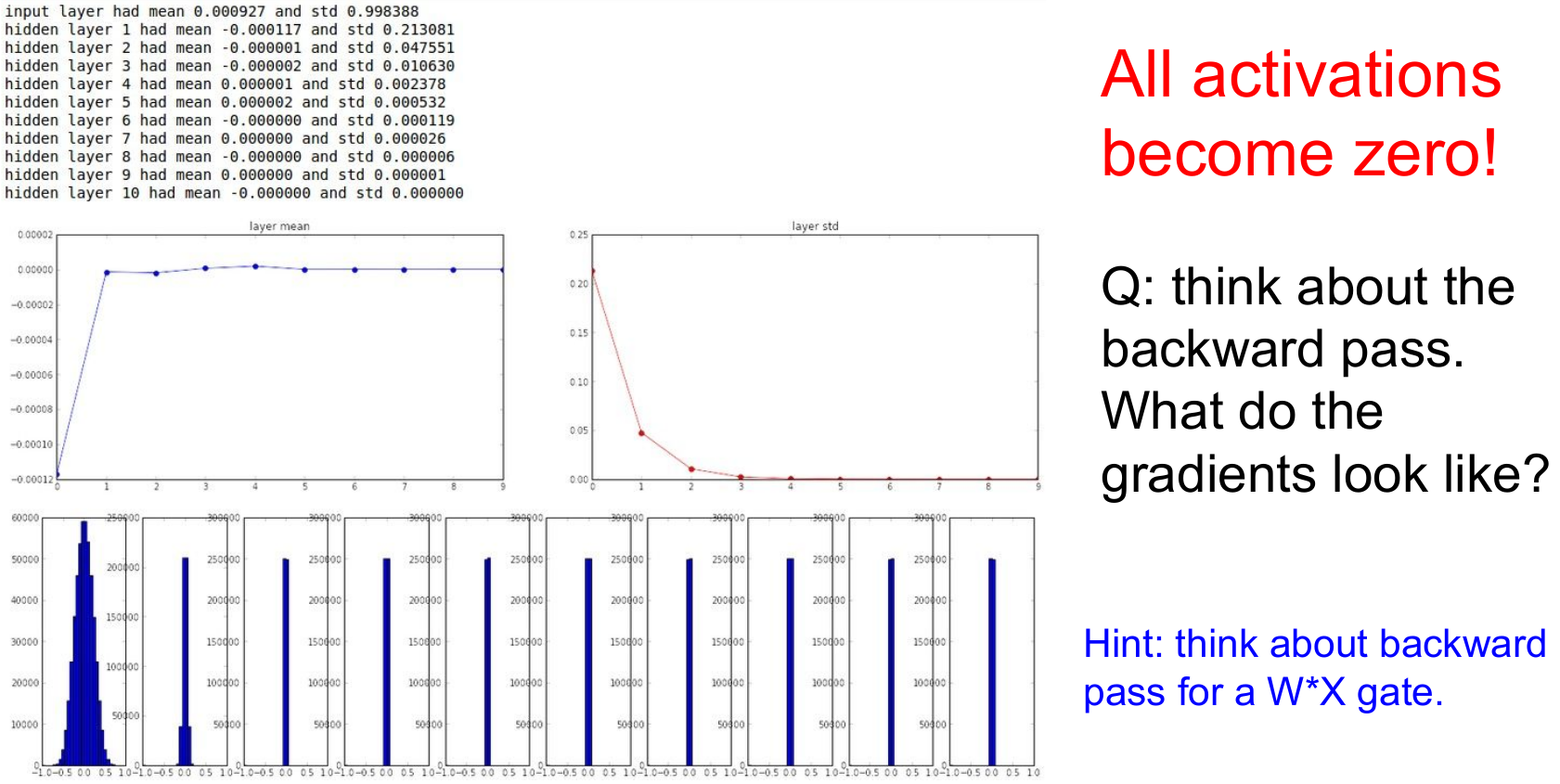
초기 가중치가 매우 작은 수치일 경우, 작은 네트워크에서는 평균을 0으로 하는 분포를 보이며 잘 작동하는것처럼 보이지만, 네트워크가 깊어질수록 편차가 0으로 수렴하는 것을 볼 수 있습니다. 너무 작은 값을 곱해 나가기 때문에 출력값이 빠르게 0에 가까워지는거죠. backward pass의 경우 역시 너무 작은 값의 기울기를 구해나가기 때문에 업데이트가 거의 일어나지 않습니다.
3-2. Initialization too big
너무 작은 수치는 좋은 선택이 아니라는 것을 알았습니다. 그렇다면 큰 값을 주면 어떨까요? 이번엔 초기 가중치값을 1로 주고 실시해보겠습니다.

반면 초기 가중치가 너무 클 경우엔 값이 발산해버립니다. 이번엔 초기 가중치를 1로 설정하겠습니다. 범위가 정해져있다면 빠르게 saturate되겠군요. tanh 함수를 activation function으로 사용하고 있기 때문에 1과 -1로 빠르게 saturate됩니다. gradient는 0이 되고 업데이트는 일어나지 않을 것입니다.
3-3. Initialization just right
그럼 어떻게 해야 하나.. 싶습니다만, 여기 한가지 대안이 있습니다. Xavier initialization을 사용하는 것입니다. 간단히 설명하면 가중치를 가우시안 정규분포에서 랜덤으로 뽑아 이를 입력 노드의 갯수로 나눠줍니다(normalization). 입력의 수가 작은 경우 작은수로 나눠 큰 값을 얻고, 큰 가중치를 곱해줍니다(반대의 경우엔 반대로!!). 이 방법은 근사적으로 동일한 출력 분포를 갖게 할 뿐만 아니라 신경망의 수렴률 또한 향상시키는 것으로 알려져 있습니다.
ReLU의 경우 위의 Xavier initialization이 효율적이지 않습니다. 출력 분산의 절반이 죽어버리기 때문입니다. 이를 해결하기 위해 2로 나눠주면 출력값의 절반이 죽어 gradient update가 멈추던 현상이 사라지고 update가 잘 진행됩니다.


요약
선 Xavier, 후 다른방식 고려
4. Batch Normalization


Gradient descent를 할때, 모두 계산하는 것은 비효율적이기 때문에 batch를 활용한다고 했습니다. 이때 스케일이 다른 feature들이 입력되어 계산된다고 하면 입력 데이터와 출력값의 분포가 달라질 수 있습니다(scale이 큰 feature는 상대적으로 gradient가 크게 나타나기 때문에 결과적으로 weight와의 연산값이 크게 나타납니다).그렇기 때문에 학습시 사용하는 batch별로 normalize해야 합니다.
*batch normalize는 선형변환이기 때문에 구조를 변화시키지 않으며 Activation map당 각각의 분산, 표준편차를 구해야 합니다.
batch normalization은 gradient vanishing이 일어나지 않게 하는 방법입니다. activation function의 구조로 gradient vanishing을 조절하는것이 아니라, 학습 과정에서 이를 해소하려 합니다.
한가지 의문이 생깁니다. 분석의 왜곡을 막기 위해 데이터를 normalize해줘야 하는데, 그렇다면 batch를 사용하는 분석에선 어떻게 normalize해야 할까요?
학습 단계에선, 좌측 그림과 같이 만약 batch당 N개의 학습 데이터와 D개의 차원이 있다면 batch당 D개의 차원별로 평균을 계산한 후 normalize 해줍니다. 결과적으로 각 배치별 input distribution(입력값의 분포)이 N(0, 1)인 정규분포를 따르게 됩니다. 이 과정을 거치면 layer별, 또는 activation별 분포가 달라지지 않게 됩니다. 일반적으로 FC layer와 Conv layer의 뒤에 위치하며, non-linear function의 앞에 위치합니다.
반면에 예측 단계에선 우리가 실제로 원하는 것은 원본 데이터에서의 W이기 때문에, 전체 데이터를 반영하기 위해 전체 데이터의 평균과 분산을 사용합니다.
batch normalization을 통해 regularization 한 후, 감마(scaling), 베타(shifting) 학습을 통해 scaling 및 shifting 실행(gradient vanishing 조절 가능)
*감마(scaling), 베타(shifting)를 다시 학습시켜서 업데이트하는 이유 : flexibility


장점
- reduces gradient vanishing & exploding
- 학습 속도 향상(Allows higher learning rates)
- 가중치 초기화 의존 감소
- 정규화 역할 수행(Acts as a form of regularization per every batch)
5. Babysitting the Learning Process
1. preprocess the data
2. choose the architecture
모델의 구조를 (대충이라도)결정
3. loss값이 잘 작동하는지 확인
규제(regularization)가 0 → 0.001일 때 변화를 관찰(loss가 증가하면 제대로 작동하는것)
4. 작은 데이터를 시험삼아 학습(sanity check, overfitting되면 제대로 작동하는것)
5. 학습을 반복하며 적절한 regularization값과 learning rate 탐색(작은 값부터 시작하여 loss가 감소하는 방향으로)
6. Hyperparameter Optimization
하이퍼 파라미터의 탐색 역시 비슷한 방식으로 진행됩니다. cross validation, log scaling등을 진행하는데요. 처음엔 rough한 idea를 얻기 위해 몇개의 epoch만 진행합니다. 이후 runnung time을 늘려가며 더 나은 하이퍼 파라미터를 탐색하는 것이죠.
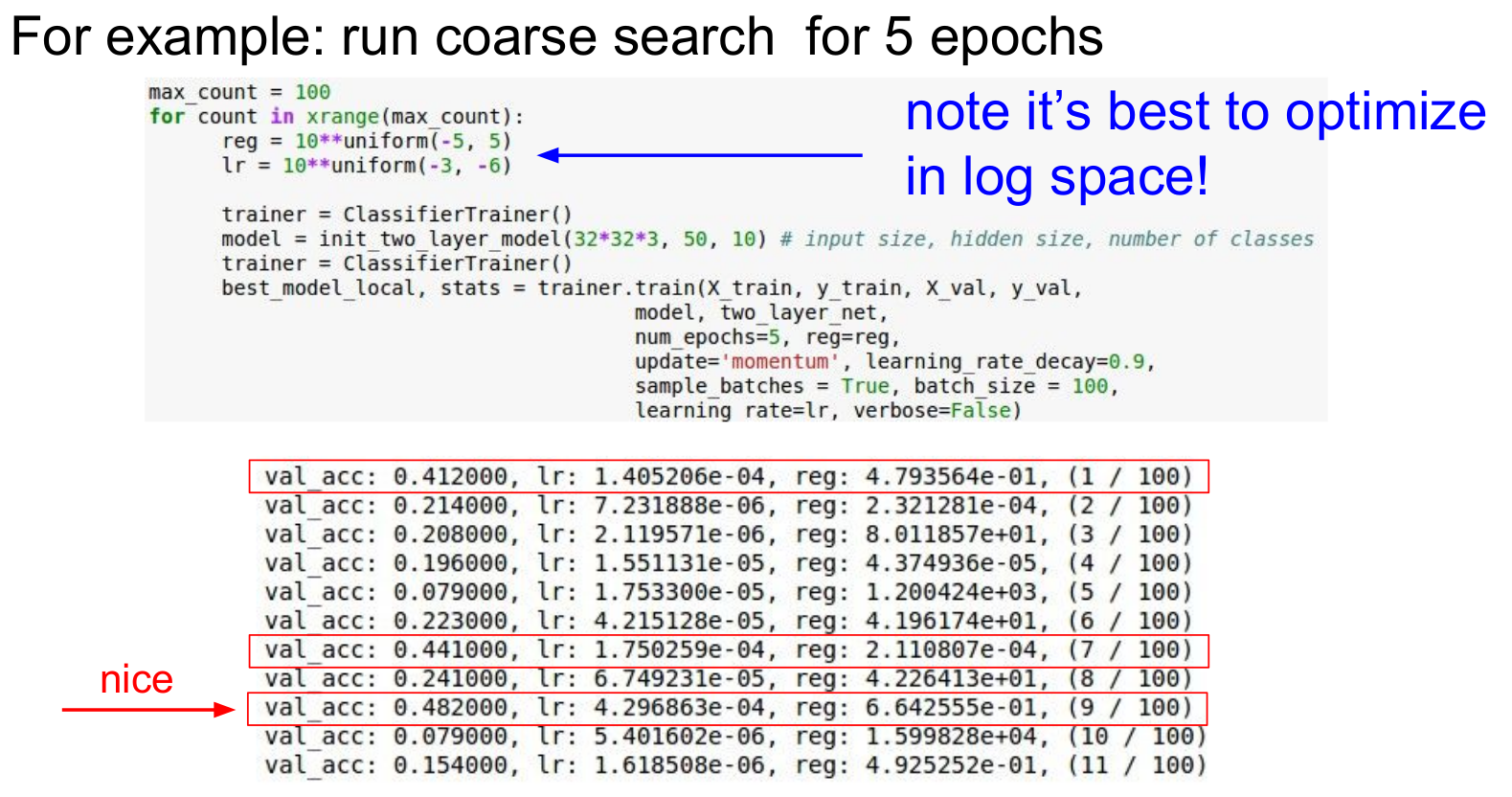
예를 들어 봅시다. 사진에서 보듯 regularization값과 learning rate값의 범위를 지정해줍니다. 이때 log scaling을 해 주는데, 이는 결과를 안정적으로 만들어준다고 합니다(note it's best to optimize in log space!). 처음 범위를 10**(-5, 5)의 범위 사이의 임의의 수로 지정하고 학습을 진행하는데, learning rate가 e-4, regularization값이 e-01인 부분에서 높은 validation accuracy가 나옵니다.

이를 기준으로 regularization값을 (-4, 0) 사이, learning rate값을 (-3, -4) 사이로 조정합니다. 이런식으로 validation accuracy가 높아지는 방향으로 수정해나가면 됩니다.

이런식으로 탐색하는 기법은 grid search와 random search 두 가지를 주로 사용합니다. 둘중에선 더 많은 경우의 수를 탐색할 수 있는 random search기법이 더 효과적입니다.(더 빠르게 더 좋은 결과를 도출)
이처럼 탐색해야하는 하이퍼 파라미터는 network architecture, learning rate, regularization값 등이 있습니다.

loss curve를 모니터링하며 탐색할 수도 있습니다. 우리가 원하는 loss그래프는 초기엔 빠르게 감소하다가 점점 감소폭이 작아지는 우측의 빨간 그래프입니다.

모니터링을 하다 보면 왼쪽과 같은 그래프가 나타날 수도 있습니다. 초반엔 전혀 학습이 일어나지 않다가 어느순간 loss값이 급격하게 감소하는 형태입니다. 이는 초기 initialization이 제대로 수행되지 않은 것으로, 초기 W값이 너무 작은 경우 발생합니다.
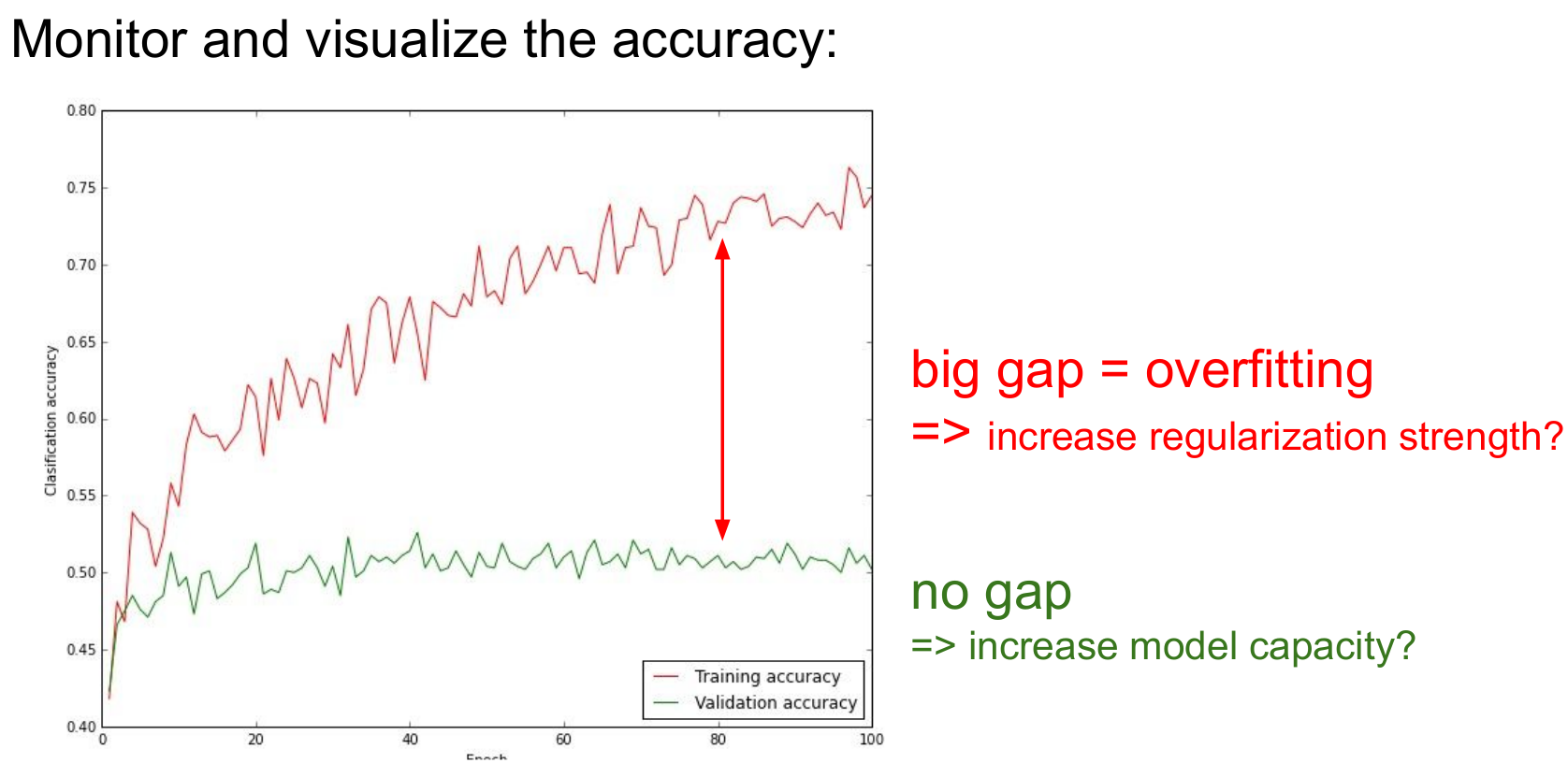
우측의 그래프는 학습이 제대로 진행되는지를 보여줍니다. 만약 두 선이 멀다면(train acc는 높아지고 val acc는 낮아짐 or train loss는 낮아지고 val loss는 높아짐) 이는 over fitting되었을 가능성이 매우 높습니다.
요약하자면
Activation Functions은 ReLU를 씁시다
Image의 경우 Data Preprocessing단계에서 zero-centered하게만 만듭시다
Weight Initialization는 Xavier init을 씁시다
Batch Normalization은 하는게 좋습니다
Hyperparameter Optimization도 중요합니다
해당 글은 스탠퍼드 대학의 CS231n(Convolutional Neural Networks for Visual Recognition)을 정리한 글임을 밝힙니다.
'Note' 카테고리의 다른 글
| Github 업로드 (0) | 2021.06.18 |
|---|---|
| DEEPML(CS231n) Lec.07 Training Neural Networks, Part2 (1) | 2021.02.21 |
| DEEPML(CS231n) Lec.05 Convolutional Neural Networks (0) | 2021.01.31 |
| DEEPML(CS231n) Lec.04_1 Backpropagation (0) | 2021.01.25 |
| DEEPML(CS231n) Lec.04_1_1 What is backpropagation really doing? (0) | 2021.01.24 |