'신경망에 대해 공부한다'는 것은 오차를 최소화하는 가중치와 편향을 찾는 것입니다. 경사 하강법을 기반으로 오차함수의 음의 기울기를 구하면, 가중치들과 편향을 어떻게 바꿔야 하는지 알 수 있습니다. 역전파는 오차 함수를 줄여나가기 위한 가장 효율적인 방법입니다.
*각 오차는 오차 함수가 각 가중치 및 편차에 얼마나 민감한지를 알려줍니다. 예를 들어 기울기가 3.2인 가중치는 0.1인 가중치에 비해 오차 함수의 출력에 32배 더 민감하게 반응합니다. 이는 곧 3.2인 가중치를 조절했을 때 오차 함수의 출력이 변하는 수치가 0.1인 가중치를 조절했을 때 변하는 양보다 32배 높다는 것입니다.
한장의 이미지의 예시를 통해 이를 보다 직관적으로 이해해 봅시다. 한 이미지의 훈련사례를 통해 가중치와 편향을 조정하는 과정에 역전파가 왜 필요한지(어떤 작용을 하는지) 살펴봅시다.
우리에게 다음과 같은 네트워크가 있습니다. 아직 훈련이 제대로 이뤄지지 않아 제대로 예측하지 못하는 듯 보입니다. 우리는 출력물이 정답 레이블처럼 나타나길 원하기 때문에, 이를 위해 가중치를 조절해 줘야 합니다. 그렇다면 우리는 어떤 가중치를 어떻게 수정해야 할까요?
*신경망은 n번째 층과 n-1번째 층의 상호작용의 합으로 구성
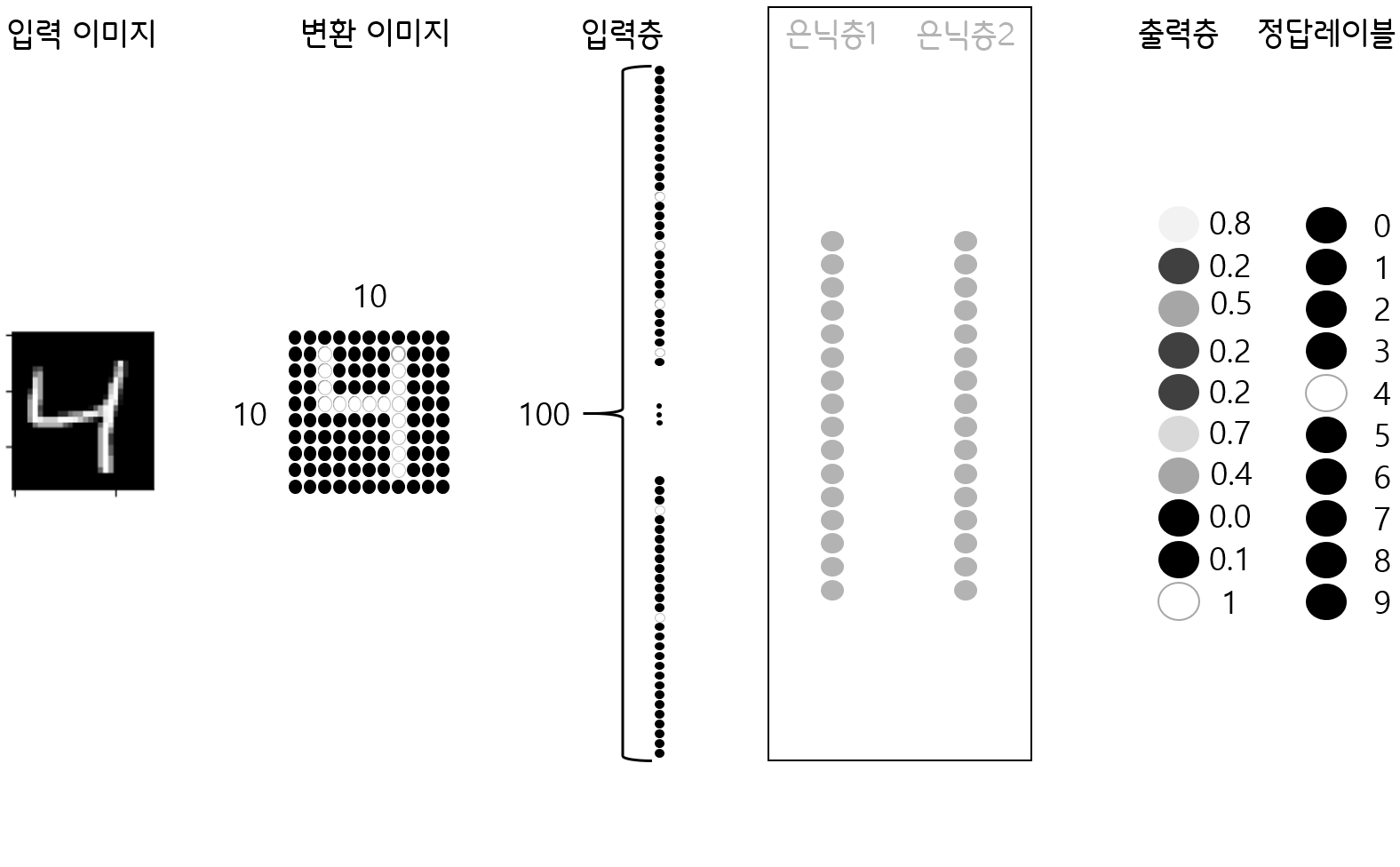
간단합니다. 우리가 원하는 4번 출력물의 수치를 높이고, 출력층의 나머지 수치를 낮춰야겠죠. 오차를 크게 만드는 출력물의 가중치값(9, 0, 5 등)은 더 크게 줄이고, 오차가 작은 출력물의 가중치(7, 8 등)는 조금만 낮춰줘도 될 것 같습니다.
이전 계층의 모든 활성화에 대한 특정 가중치 합계와 편향은 시그모이드 함수나 다른 ReLU와 같은 활성화 함수와 연결되어 있습니다. 이를 바탕으로 해당 레이블의 출력 값을 높일 수 있는 가중치를 조절할 수 있는 방법은 세 가지가 있습니다. 편향을 증가시키거나, 가중치를 증가시키거나 이전 레이어의 활성도를 변경하는 것이죠.
Increase b
Increase Wi
Change ai
우리가 활성화를 원하는 4번 레이블과 연결된 뉴런에 초점을 맞춰 봅시다. 가중치를 조절할 때, 동일한 크기만큼 가중치를 조절해도 이전 단계의 활성화 정도에 따라 4번에 미치는 영향력이 다릅니다(가중치와 활성도를 곱하니까요!). 가령 가중치를 똑같이 10만큼 올린다고 했을 때, 활성화가 잘된 뉴런(밝은색)이 출력층에 더 큰 영향을 미칠 것입니다.

만약 우리가 이전 단계의 활성화 정도(밝기로 표현)를 바꿔준다면, 4번이 보다 명확하게 보일 것입니다. 이를 위해 양의 가중치 신경을 전부 밝게, 음의 가중치 신경은 전부 어둡게 바꿔준다면, 4번 뉴런은 더욱 활동적으로(1에 가깝게) 될 것입니다.
*4번에 대한 양의 가중치값은 해당 train data의 loss score를 작게 만들고, 음의 가중치는 loss score를 크게 만듦
추가적으로 마지막 레이어의 정답 이외의 다른 모든 뉴런들이 덜 활동적이면 좋겠죠? 따라서 위에서 가중치를 영향도에 비례해 바꾼 것처럼, 가중치의 변화량에 따라 활성화 정도를 바꿔주는 겁니다. 이처럼 우리가 어떤 방향으로 수치들을 개선해 나가야 하는지 기록해두는 것이 중요합니다.
이제까지 숫자 4의 출력 뉴런에 집중해서 프로세스를 이해해 보았습니다. 지금까지의 과정은 4번 뉴런이 원하는 방향일 뿐, 크게 보면 이러한 과정을 전체 네트워크에 적용해야 합니다. 오차 함수는 수만가지의 train data별 오차를 평균화하기 때문에 단일 경사 하강법 단계에서 가중치와 편향을 조정하는 방식 역시 train data에 따라 다릅니다.
각각의 출력 뉴런들은 마지막층과 바로 이전 층에 대한 정보를 가지고 있습니다. 이 과정을 출력층의 모든 뉴런에 반복해줘야 합니다. 10개의 출력 뉴런에 대한 욕구(가중치와 활성도에 비례한 각 뉴런들이 나아가야 할 '방향')가 누적된다면, 그리고 이를 모두 합하면, 가중치를 어떻게 변화시키는 것이 효율적인지 알 수 있을 것입니다. 이 부분에서 역전파의 아이디어가 시작됩니다.

위의 과정을 거쳐 우리는 n-1번째 층에서 n번째 층의 방향으로 일어나는 변화의 뉘앙스를 알 수 있습니다. 그리고 이것을 기록해 놓는다면, 해당 손실값을 구하는 데 사용된 가중치와 편향, 그리고 활성도를 재귀적으로 계산해 나갈 수 있습니다. 모든 가중치와 편향(n번째 레이어와 n-1번째 레이어의 상호작용의 수의 합 + 노드별 편향의 수)만큼 해당 작업이 반복되어야 하며 그 결과 한 이미지(여기서는 4의 이미지)가 각 가중치와 편향을 어떻게 바꿔가길 바라는지를 알 수 있습니다. 이를 통해서 우리의 네트워크는 이미지를 4로 분류하기 위한 인센티브를 얻게 됩니다. 따라서 우리는 모든 트레이닝 예제에서 이와 같은 수치들을 얻어야 하며, 이를 위해 모든 예제에 대해 동일한 백드롭 루틴을 수행해야 합니다. 각자가 가중치와 편향을 어떻게 바꾸고 싶은지를 기록하고, 원하는 변화의 평균을 구합니다.(w0에 대한 모든 트레이닝 데이터의 평균, w1에 대한 모든 트레이닝 데이터의 평균, ... , wn에 대한 모든 트레이닝 데이터의 평균)
*그리고 이러한 과정의 이해는 Cost function의 음의 기울기에 대한 개념과 연결됩니다.
이런 과정은 개개의 단계별로 계산해 나가야 하기 때문에 비용이 매우 많이 소모됩니다. 이를 해결하기 위해 mini batch를 사용합니다.
우선 학습 데이터를 무작위로 섞은 다음 전체 mini batch(hyper parameter)로 나눠줍니다. 그런 다음 경사 하강의 step을 계산합니다. 이 과정으로 나온 값이 실제 기울기가 될 수는 없습니다. 추출한 크기만큼의 표본으로 계산하기 때문인데, 정확하진 않지만 나쁘지 않은 근삿값을 제공하고 속도가 현저히 빠릅니다. batch size만큼의 연산 결과(gradient)만큼 하강하고 다음 batch의 gradient를 연산하기 때문입니다. 이것이 Stochastic gradient descent(확률적 경사 하강)의 개념입니다.
요약하자면
역전파는 가중치를 어떤 방식으로 바꿔야 하는지 결정하는 알고리즘으로, 단순히 방향을 결정하는 것이 아닌 효율성의 측면(특히 비용 감소의 효율)까지 고려하는 알고리즘입니다. 이를 위해 모든 가중치의 모든 변화를 계산해서 평균을 내야 하는데, 이는 너무 오래 걸립니다. 이를 극복하기 위해 mini batch를 사용합니다.
CS231n 4강의 내용 이해를 위한 공부입니다. 3BLUE1BROWN의 유튜브를 정리한 내용임을 밝힙니다.
'Note' 카테고리의 다른 글
| DEEPML(CS231n) Lec.05 Convolutional Neural Networks (0) | 2021.01.31 |
|---|---|
| DEEPML(CS231n) Lec.04_1 Backpropagation (0) | 2021.01.25 |
| DEEPML(CS231n) Lec.03_2 Optimization (0) | 2021.01.22 |
| DEEPML(CS231n) Lec.03_1 Loss Function (2) | 2021.01.10 |
| DEEPML(CS231n) Lec.02_2 Linear Classification (0) | 2021.01.04 |