이전 강의까지 우리는 가중치를 조절하는 방법에 집중해서 공부했습니다. 그리고 그 과정에서 '괴랄한' 모델들을 얼핏 본 것 같습니다. 오늘은 이미지 학습에 주로 쓰이는 '괴랄한' 모델 중 하나인 CNN(Convolutional Neural Networks)에 대해 공부할 것입니다.
1. FC(Fully Connected Layer)와 Conv(Convolution Layer)의 차이

우리가 이제까지 공부한 linear classifier를 간단하게 도식화하면 위의 그림 1과 같습니다. 이미지를 쭉 늘여서 한줄로 만들어서 가중치와 곱해줬었죠? 그 결과 이미지에 대한 하나의 Score값으로 표현되었습니다.
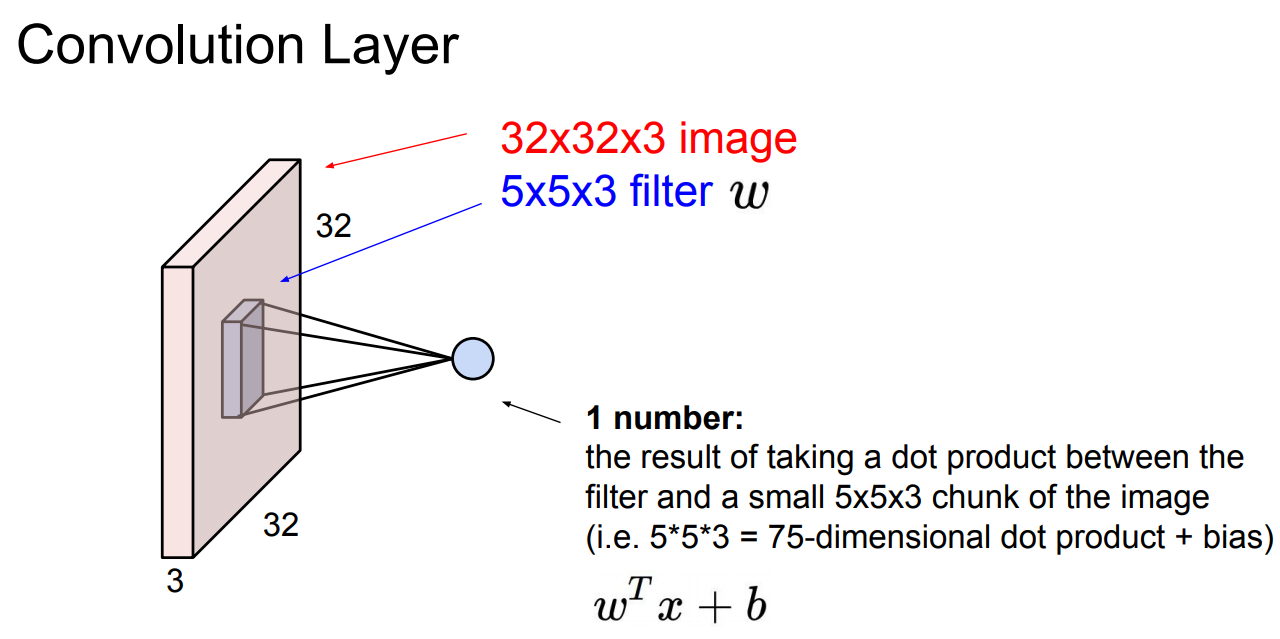
Conv는 구조부터 차이가 있습니다. 그림 2와 같이 원본 그대로의 형태를 유지(공간의 구조에 대한 정보를 유지하는 것입니다!)하면서, filter를 사용해서 레이어를 훑습니다(표현이 이상하지만 뒤에 설명을 보시면 '훑는다'는 표현이 이해되실겁니다). 한 연산의 과정을 거치면 하나의 숫자를 얻는데, 이는 필터의 dimensional dot product의 크기 * 채널수 + 분산의 결과입니다(위의 예에서 5 * 5 * 3 + 1).
이때 필터는 다음과 같은 조건이 있습니다.
1. Convolution Layer와 채널수가 같아야 한다.
2. 크기는 제한이 없지만, Convolution Layer의 크기를 넘으면 안 된다.
2. Convolution Layer의 성질
앞에서 Layer를 필터로 훑는다고 했습니다. 1개의 필터로 이러한 과정을 거치면 1채널의 activation map 1개를 얻게 됩니다. 이 과정은 다음과 같습니다.

하나의 필터를 거칠 때마다 하나의 activation map이 나옵니다. 그리고 필터는 각각 다른 특징을 추출합니다.

만약 5 * 5 * 3인 필터가 6개 있다면, 그림 4와 같이 28 * 28 사이즈의 activation map 6장이 나올 것입니다.

이미지를 다중 필터로 훑고, 활성화 함수를 거치는 것이 하나의 단계로 구성됩니다. 단계를 거듭할수록 이미지의 크기가 작아지는 것이 보입니다. 첫 단계에서 5*5*3의 필터 6개로 훑었기 때문에 두 번째 단계에서 6채널(6장)이 되었고, 두번째 단계에서 10개의 필터로 훑었기 때문에 10채널(10장)로 구성됩니다.
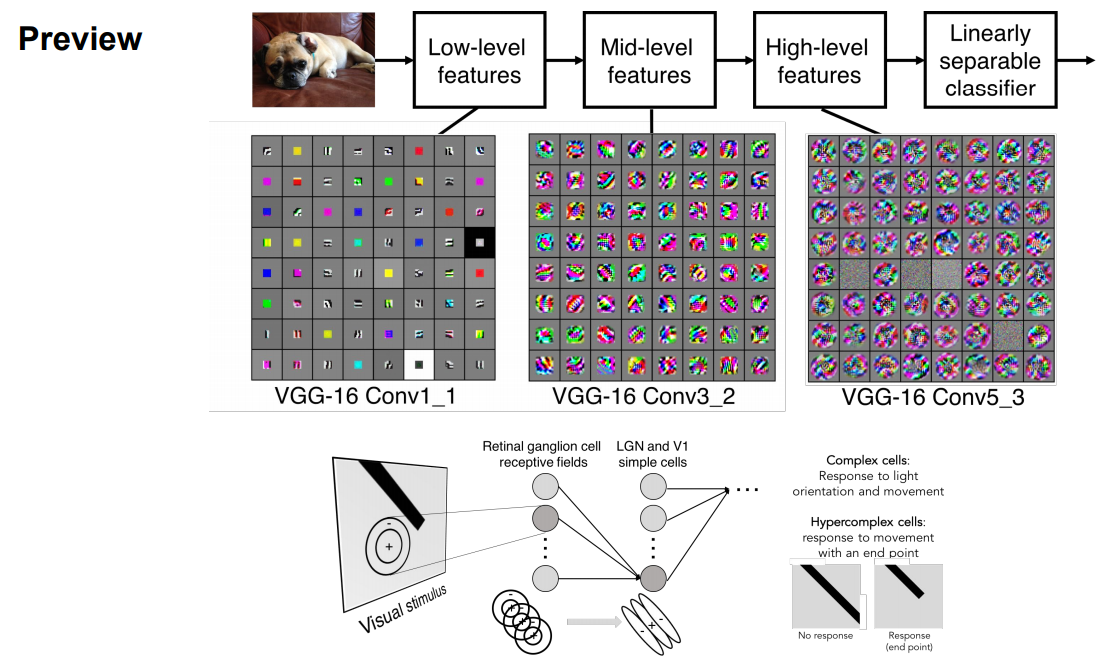
필터를 시각화하면 그림 6과 같은 모양이 될 것입니다. 필터를 거칠수록 저 차원에서 고차원의 특징을 추출합니다(6장의 필터일 때, 1번 필터에서는 점을, 2번 필터에서는 선을, ... , 6번 필터에서는 형태를 추출).
미리 살펴보자면, Convolution Neural Networks는 결과적으로 다음과 같은 구조를 갖게 됩니다.

3. 필터(receptive field)의 동작 원리와 연산과정
다음 이미지는 필터의 동작 과정을 직관적으로 보여줍니다. 필터는 좌상단에서 시작해, 오른쪽으로 훑어가며 특징을 추출합니다. 한 장의 필터가 이미지에 한번 닿을때마다, 하나의 값을 추출(내적)합니다. 이 값이 모이면 한장의 activation map이 출력됩니다.


연산의 결과는 어떻게 나타날까요? 쉽게 알 수 있게 7*7픽셀의 이미지를 3*3 필터로 훑어간다고 생각해 봅시다. 앞서 언급한 대로 좌상단부터 훑어갑니다. 직접 손으로 그려보면 쉽게 몇 번의 연산을 하는지 알 수 있습니다. 제가 해본 결과 4회 우로 이동하고 5회의 연산을 하는군요(시작 부분도 연산해야죠!). 7*7의 이미지니까 세로로도 같은 횟수의 연산을 하겠죠? 결과적으로 5*5의 출력물을 얻을 수 있습니다.

7칸이면 5회 연산이라.. 뭔가 일반화할 수 있을 것 같습니다. 간단하게 4*4의 이미지를 2*2 필터로 훑는다고 생각해봅시다. 2회 이동에 3번의 연산을 하게 되는군요. 최종 출력물의 크기는 3*3입니다. 뭔가 보이십니까?
7과 3을 가지고 5를 만들려면 (7-3) + 1 하면 되겠군요. 4와 2를 가지고 같은 방식으로 3을 만들 수 있을까요? (4-2) + 1로 동일하군요!! 뭔가 보입니다.
여기서 한 가지 의문이 생깁니다. 이동은 반드시 한 칸만 해야 할까요? 아닙니다. 이동하는 칸수는 하이퍼 파라미터로, stride라고 합니다. 7*7 이미지에 5*5 필터를 적용하여 2칸씩 이동해볼까요? 이번엔 출력 이미지가 3*3이 되겠죠?(2회 이동에 3회 연산입니다!)
우리가 알아낸 패턴을 적용해 보겠습니다. (7-3) + 1은 5였는데요.. 하지만 달라진 점이 있습니다. 2칸씩 이동했다는 것이죠. 7-3과 1을 가지고 3을 만들 수 있는 방법이 있을까요? 바로 7-3을 2로 나눠주는 것입니다. 그럼 2+1 = 3이 되겠죠?
여기서 한 가지 패턴을 찾을 수 있을 것 같습니다. 이미지의 한 변의 크기를 N, 필터의 한 변의 크기를 F, 이동하는 칸 수를 stride라고 할 때, 공식은 다음과 같습니다.
Output size = (N - F / stride) + 1
4. Padding(zero padding)
만약 3칸씩 이동한다면 어떻게 될까요? (7-3)/3 + 1이 되고 결과 이미지는 2.33*2.33이 될 것입니다. 칸수는 정수로 나와야겠죠? 따라서 3칸 이동은 안된다는 것을 알 수 있습니다. 굳이 3칸 stride를 하고 싶다면 1칸 padding을 하면 됩니다. 그럼 우리의 이미지를 둘러싼 0으로 9*9 크기의 이미지가 생길 것입니다. (9-3)/3 + 1 = 3으로 3*3의 출력물을 얻을 수 있을 것입니다.
여기서 padding의 개념이 나옵니다. padding은 이미지의 외곽에 0으로 구성된 칸을 채워 넣는 것입니다(zero padding). padding을 하는 이유는 크게 두 가지가 있습니다.

먼저 이미지의 축소를 막아줍니다. 필터를 거친 이미지는 항상 작아졌습니다. 7*7 이미지를 3*3 필터로 연산한 출력 값은 5*5 이미지가 되었죠. 이미지가 축소된다는 건 원본 이미지로부터 왜곡이 생긴다는 것입니다. 이때 1칸 패딩을 한다면? (9 - 3) / 1 + 1로 7*7 이미지가 유지되었습니다!! 이처럼 우리는 원본의 형태를 유지하기 위해 padding을 사용할 수 있습니다.(잘 사용하면 출력값의 크기를 조절할 수도 있겠죠!)
두 번째는 연산의 불균형을 해소할 수 있습니다. 이미지의 연산과정 중 외곽의 픽셀은 연산이 1회밖에 되지 않아 내부의 픽셀에 비해 평가절하됩니다. 따라서 padding을 해줌으로써 이러한 평가절하를 완화해줄 수 있습니다.
일반적으로
3*3 필터에는 1칸의 zero pad를
5*5 필터에는 2칸의 zero pad를
7*7 필터에는 3칸의 zero pad를
사용합니다.
연산을 거치는 파라미터(가중치)의 수는?
3개의 채널을 가진 5*5 필터로 연산합니다. 따라서 연산에 활용되는 파라미터의 수는 (5*5*3+1(bias))*10으로 760개입니다. 하나의 필터에 25개의 파라미터*3층으로 75에 1층마다 bias 1을 더해줍니다. 76*10의 필터로 총 760개의 파라미터를 갖게 됩니다.
앞에서 우리는 필터의 개수에 따라 이미지의 차원이 바뀐다는 것을 알 수 있었습니다. 여기서 한발 나아가 차원을 마음대로 조정할 수도 있습니다. 7*7*3의 이미지에 1*1(*3)의 필터, stride 1을 사용하면, 출력 이미지의 크기는 동일하게 유지되겠죠?((7 - 1) / 1 + 1 = 7). 이때 필터를 1개만 쓰면? 7*7*1의 이미지가 되었습니다! 이처럼 차원 축소의 방법으로 활용할 수 있습니다.
5. FC와 CONV의 한 점(시점)에서의 차이


FC의 출력값의 한 점(1 number, dot product)은 입력 이미지의 전체 연산을 통한 한 클래스의 결괏값입니다. 반면 CL의 5중 필터를 거친 한 시점의 dot products(5 neurons)는 한 시점의 입력 이미지의 5가지 서로 다른 특징을 나타냅니다. 풀어쓰자면 FC의 한 점은 고양이로 예측하는 점수를 나타내는 것이라면, CONV의 한 시점은 입력 이미지의 특정 부분(고양이 귀)의 여러 특징(점, 선, 각도, 방향, 색 등)을 나타냅니다.
이 차이점을 바탕으로 서로 뭐가 다른지 살펴봅시다. 우선 같은 이미지(우리의 고양이 이미지를 예로 들어볼까요?)를 FC는 한 줄로 늘려서, Conv는 형태를 유지해서 연산한다고 했습니다. 우리의 목표는 컴퓨터가 고양이라고 말하게 하는 것이었습니다. 두 가지 모두 고양이라고 출력하는 게 가능하다면, FC로만 수행해도 될 텐데 굳이 이 어렵고 복잡한걸 왜 읽고 있어야 할까요?
간단합니다. conv가 더 잘 맞춥니다. FC는 이미지의 각 픽셀에서의 특징을 점수화하여 훈련합니다. 새로운 이미지가 들어왔을 때 같은 위치의 같은 특성을 갖는 데이터만 명확히 판단할 수 있습니다. 바꿔 말하면 유사한 각도의 다른 이미지를 오분류할 가능성도 높은 것입니다. 반면에 Conv는 필터를 거치며 점점 다양한 고차원의 특성을 추출하기 때문에 일반화해서 판단할 수 있습니다.
또 연산의 양이 훨씬 줄어듭니다. 성능적인 면, 그리고 효율성의 면에서 모두 Conv가 우월한 거죠.
대신 Conv는 특징을 추출할 뿐 결과가 어떤 class에 속하는지 판단할 수 없습니다. 따라서 Conv의 마지막에 FC를 추가해 class를 분류해줘야 합니다. 다음 그림처럼요.

6. Pooling Layer
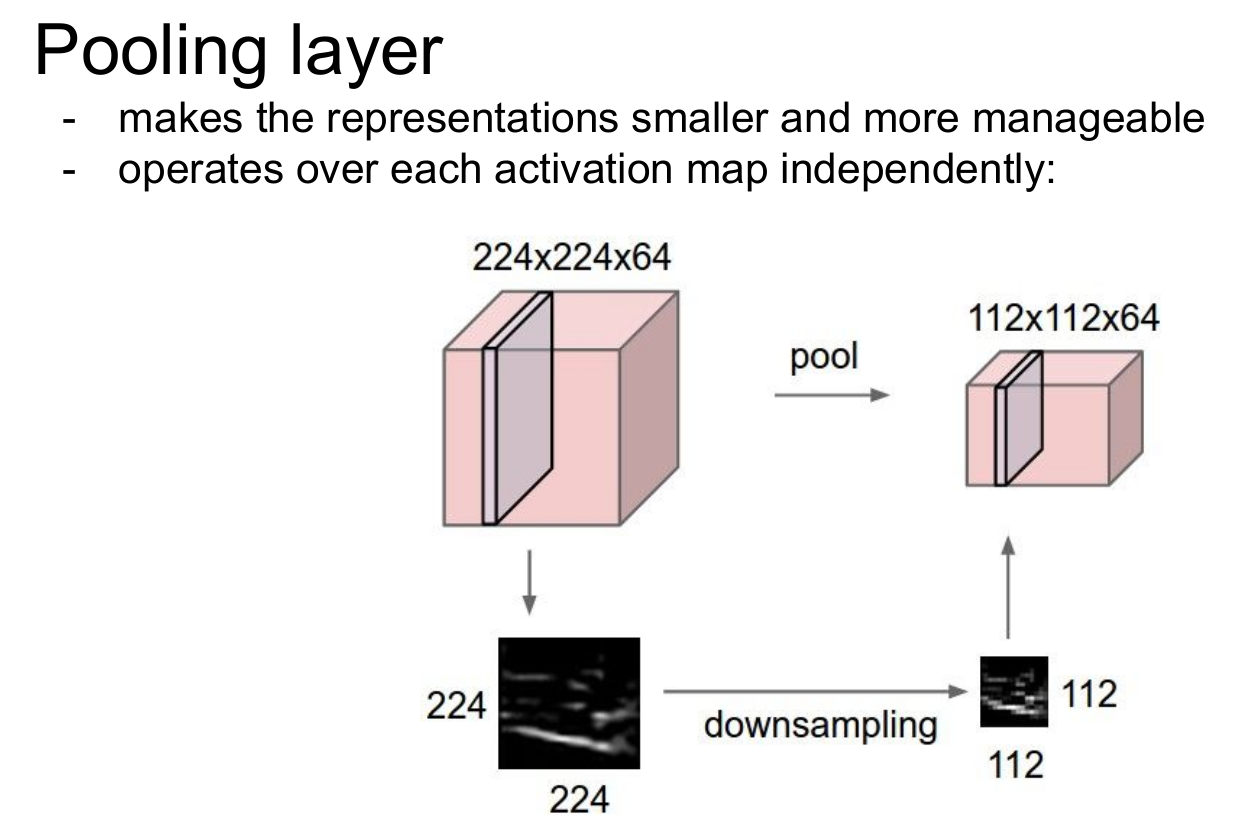
Pooling Layer는 activation map을 입력으로 받아 크기를 줄여 특징을 강화-추출하기 위한 용도로 사용합니다. 연산을 간소화해주는 역할도 수행합니다. 이미지의 픽셀을 줄이면 같은 크기의 필터에 더 많은 부분을 투영할 수 있습니다. 그렇다면 pooling을 반복할수록 점점 전체적인 특징을 추출(추상화)하는 것이 가능해질 것입니다.

Pooling에는 여러 방식이 있는데, 그중 가장 많이 사용하는 Max pooling을 알아봅시다. 이번엔 빈 필터를 준비합니다. 2*2의 형태만 가지고 있는 필터입니다. 4*4의 이미지에 stride를 2로 주고 적용한다면, 왼쪽 그림처럼 4 구역으로 구분할 수 있습니다. 각 구역별 Max값만 추출하여 필터를 채워 넣습니다. 이로써 필터를 적용한 구역별 가장 큰 특징만 추출되었습니다. 출력물을 구하는 공식은 다음과 같습니다. W1*H1*D1의 이미지가 있을 때 pooling layer의 filter의 변의 크기를 F, stride를 S로 설정한다면
output size = W2*H2*D2
W2=(W1-F)/S + 1
H2=(H1-F)/S + 1
D2=D1
일반적으로 아래와 같이 설정합니다.
F = 2, S = 2
F = 3, S = 2
여기까지 Conv Network에 대해 공부했습니다. Conv Network는 특히 이미지 처리에서 월등한 성능을 보여줍니다. Alex Krizhevsky는 「ImageNet Classification with Deep Convolutional Neural Networks」에서, 다음 두 가지 가정을 통해 왜 CNN이 이미지 학습에 잘 들어맞는지를 설명합니다.
stationarity of statistics : 같은 특징이라면 한 데이터 내의 다른 부분에서도 동일할 것이며, 이는 다른 데이터에서도 동일하게 나타날 것입니다. 이는 한 가지 특징을 추출하면 다른 각도, 위치, 크기에 모두 적용할 수 있습니다(파라미터 공유).
and locality of pixel dependencies : 픽셀 데이터의 특성상 한정된 범위 안에서 종속성을 갖는다는 의미로, 인물사진에서 얼굴 전체가 아닌 눈, 코, 입의 객체를 따로 구분하게 하여 특징을 인접한 픽셀에 한정하게 합니다. 이는 다른 특징을 추출할 때 오류를 줄일 수 있습니다.
요약하자면
ConvNet은 Conv, pool. FC layer들을 쌓은 것입니다.
Filter는 작게, 구조는 깊게 쌓는 방식이 트렌드입니다.
Pool이나 FC레이어는 제거하는 것이 트렌드입니다(Conv만으로 구성).
일반적인 구조는 C[(CONV-RELU)*N-POOL?]*M-(FC-RELU)*K,SOFTMAX이며
N은 5를 넘지 않고, M은 제한이 없으며, 0 <=K <=2가 일반적입니다.
but recent advances such as ResNet/GoogLeNet challenge this paradigm
해당 글은 스탠퍼드 대학의 CS231n(Convolutional Neural Networks for Visual Recognition)을 정리한 글임을 밝힙니다.
'Note' 카테고리의 다른 글
| DEEPML(CS231n) Lec.07 Training Neural Networks, Part2 (1) | 2021.02.21 |
|---|---|
| DEEPML(CS231n) Lec.06 Training Neural Networks, Part1 (0) | 2021.02.12 |
| DEEPML(CS231n) Lec.04_1 Backpropagation (0) | 2021.01.25 |
| DEEPML(CS231n) Lec.04_1_1 What is backpropagation really doing? (0) | 2021.01.24 |
| DEEPML(CS231n) Lec.03_2 Optimization (0) | 2021.01.22 |