지난 강의에서 전반적인 내용을 살펴봤다면, 보다 자세한 내용을 다루는 강의입니다. 크게 Fancier optimization, Regularization, Transfer Learning에 대해 배웁니다.
Optimization
최적화의 문제에서, SGD가 원하는 결과를 내는데 도움을 준다고 했습니다. 그렇다면 optimization은 '묻따말' SGD를 쓰면 되는걸까요?

아쉽게도 SGD를 쓰기엔 몇가지 치명적인 문제점이 있습니다. 만약 loss가 한 방향으로만 빠르게 변화하고 다른 방향으로 느리게 전개된다면 어떤 결과가 나올까요? 위 그림은 수직방향으로 빠르게 변화하는 반면, 수평으로는 느리게 변화합니다. 이런경우 수직방향으로 zig-zag현상이 발생합니다. 학습을 방해하죠.
문제는 또 있습니다. 만약 우리의 loss function에 local minima나 saddle point가 있다면 어떻게 될까요?

우리의 학습은 gradient가 작아지는 방향으로 진행되어야 하는데, local minima의 경우 현재의 위치가 최솟점이라고 착각하여 학습을 멈출 우려가 있습니다. 또 saddle point의 경우 변곡점에 속하게 되어 순간 기울기가 0이 되는 지점에서 학습을 중단할 가능성이 있습니다. 특히 local minima에 비해 saddle point가 적을것으로 보이지만, 실제 loss function에서는 saddle point가 더 자주 관찰되며 특히 고차원으로 갈수록 어디에나 존재한다고 볼 수 있습니다.

SGD에서 gradient는 mini batch를 바탕으로 하기 때문에 noise가 끼어있을 수 있습니다. 전체 데이터를 사용하는 것이 아니기에 순간의 방향을 판단할 뿐 전체적인 흐름과 일치하지 않기 때문이죠.
1. Fancier Optimization
1-1. momentum 계열(방향)
1-1-1. SGD + Momentum
위의 문제를 해결해줄 수 있는 방안으로 우선 SGD에 Momentum을 추가해 주는 방법이 있습니다.

쉽게 말하면 기존의 SGD에 속도의 개념을 추가해 줄 뿐입니다. 진행 방향으로의 속도를 추가해준다면, 관성으로 인해 어느정도의 local minima나 saddle point에서 탈출하거나, 또는 어느정도의 'noise'는 상쇄할 수 있을 것입니다.
1-1-2. Nesterov Momentum

위의 그림에서 Momentum update는 현재 위치에서의 Velocity와 gradient를 계산하여 이를 결합하는 방식을 사용하는 반면, Nesterov Momentum은 현재 위치에서 Velocity만 계산하고 이동 위치에서 gradient를 계산하여 actual step을 구하는 방식입니다. Nesterov Momentum은 SGD+Momentum에 비해 빠르고 convex(볼록한) optimization에서는 뛰어난 성능을 보입니다. 고차원 딥러닝에서는 non-convex한 모양(saddle point의 사례)이 많기 때문에 잘 쓰이지 않습니다.
*velocity의 초기값은 0(하이퍼 파라미터가 아님)
*좁고 깊은 minima는 일반화를 통해 넓고 얕은 minima로 바꿔주는것이 좋음(robust)
1-2. Ada계열(보폭)
1-2-1. Adagrad

코드해석
- 우선 grad_squared값을 0으로 초기화합니다.
- 그리고 while문을 사용해 반복합니다.
- dx는 현재 지점 x에서 계산한 gradient값입니다.
- dx를 이용해 grad_squared를 구합니다. dx를 제곱하여 계속 더해나갑니다. 이 grad_squared가 x를 구할 때 분모로 들어가는데, while문이 실행될때마다 누적되어 지속적으로 커지니 x값의 이동 정도가 점점 작아집니다.
- dx 를 np.sqrt(grad_squared)로 나눈값에 learning rate를 곱하여 초기 x값에서 뺍니다.
- 이를 활용해 다음 x값을 찾고 2번으로 돌아가 이 과정을 반복합니다.
세 번째로 AdaGrad라는 방법이 있습니다. adaptive gradient라는 이름처럼, 각 매개변수별로 적응하듯 확률을 조정해 나가는 방식입니다. 가속의 개념을 도입할 때 momentum 대신 gradient squared term을 이용합니다. 학습중 계산되는 gradient값을 제곱하여 계속 더해 나가며, 한 시점에서 계산된 gradient값을 squared gradient로 나눠줍니다. 여기서 알 수 있듯이 계산을 해나갈수록 분모가 점점 커지기 때문에 갈수록 탐색 속도가 느려집니다. convex한 경우 학습이 잘 이루어지지만 딥러닝은 말씀드린대로 non-convex 한 구간이 많습니다. 따라서 학습이 제대로 이루어 지지 않는 경우가 많을 것입니다. 이를 해소하기 위해 RMSProp이 도입됩니다.
1-2-2. RMSProp

코드해석
- 우선 grad_squared값을 0으로 초기화합니다.
- 그리고 while문을 사용해 반복합니다.
- dx는 현재 지점 x에서 계산한 gradient값입니다.
- dx를 이용해 grad_squared를 구합니다. 다만 decay rate를 grad_squared에 곱해주고 1-decay_rate를 dx^2에 곱해서 두 항을 더해줍니다.
- dx 를 np.sqrt(grad_squared)로 나눈값에 learning rate를 곱하여 초기 x값에서 뺍니다.
- 이를 활용해 다음 x값을 찾고 2번으로 돌아가 이 과정을 반복합니다.
AdaGrad를 변형시킨 것으로 누적된 squared gradient에 decay rate(일반적으로 0.9 또는 0.99)를 곱해주고 1-decay에 현재 gradient에 제곱한 값을 더해줍니다. 이렇게 하면 이전 시점의 gradient를 더 크게 반영하여 무조건 속도가 느려져 학습이 멈추는 구간이 생기는 현상을 극복할 수 있습니다.
1-3. Adam
위의 속도와 보폭을 고려한 두 방식 모두 장단점이 있습니다. 그렇다면 이 두 방식의 장점을 결합한다면 어떨까요? 이러한 아이디어의 결과로 우리는 제대로 된 방향으로 진행하며 적절한 보폭으로 최적화를 진행하는 optimizer, Adam을 사용할 수 있게 되었습니다!

위 그림은 Momentum계열의 아이디어와 Ada계열의 아이디어를 섞어놓은 모습입니다. 처음 등장한 개념인 first moment와 second moment는 각각 실제 gradient의 기대값 E(gradient)와 E(gradient^2)의 추정치를 나타냅니다. 분모에 1^-e7의 값을 더해주는 것은 분모가 0이 되지 않도록 매우 작은 숫자를 더해주는 것입니다.
그러나 Adam(almost)의 그림처럼 Momentum과 Ada의 개념을 도입하는 것으로 식이 완성되는 것이 아닙니다. 우선 위의 코드대로 진행했을 때 첫 스탭이 어떻게 진행되는지 살펴봅시다.
first_moment는 0, beta1은 0.9로 설정되어 있습니다. Momentum부분을 보면 beta1*first_moment는 0이 될 것이고 beta1은 1에 가깝게 설정되어 있기 때문에 1-beta1*dx의 값이 0에 가깝게 저장될 것입니다.(first_moment)
이 경우 해당 값이 x의 업데이트에 사용된다고 하면 분자가 너무 작은 값으로 설정되어 매우 작은정도밖에 이동하지 못할 것입니다(업데이트가 거의 일어나지 않음).
second_moment의 값이 0, beta2의 값이 0.99로 설정되어 있습니다. Momentum부분을 보면 beta2*second_moment는 0이 될 것이고 beta2은 1에 가깝게 설정되어 있기 때문에 1-beta2*dx^2의 값이 0에 가깝게 저장될 것입니다.(second_moment)
이 경우 해당 값이 x의 업데이트에 사용된다고 하면 분모가 너무 작은 값으로 설정되어 발산해 버릴 것입니다(업데이트가 일어나지 않음).

따라서 위와같은 문제점을 보완하기 위해 bias correction부분을 추가해 줍니다. 해당 부분이 추가되면 두가지 경우를 모두 완화해 준다고 합니다. 일반적으로 초기 설정값은 beta1은 0.9, beta2는 0/999, learning_rate는 1e-3이나 5e-4가 활용된다고 합니다.
1-4.그 외 방법

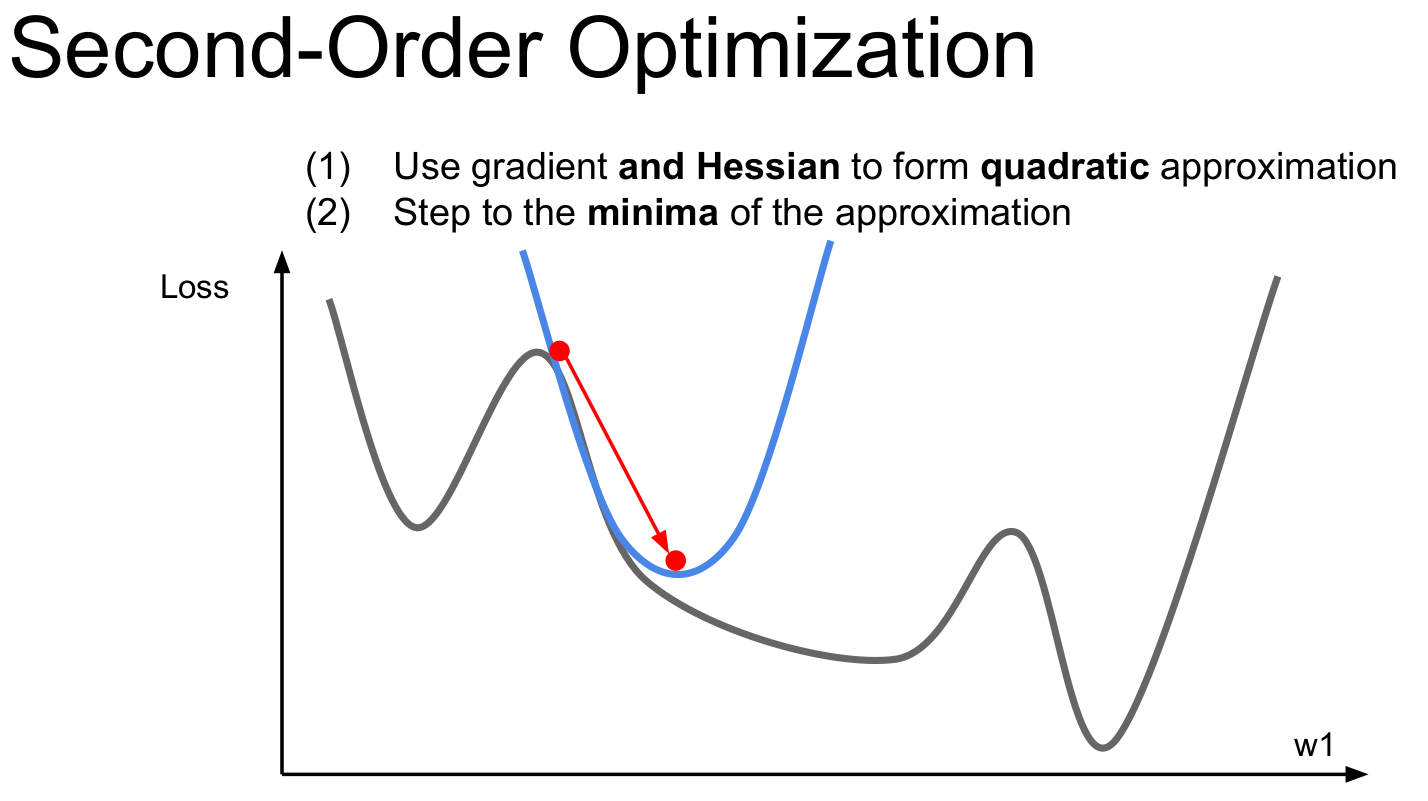
이외에도 학습이 정체되는 구간에서 learning rate를 낮춰서 학습을 촉진시키는 learning rate decay, 2차미분값을 활용하여 최솟값으로 바로 찾아가는 second order optimization등의 방법이 있다고 합니다.
2. Regularization

2-1. Model Ensembles
앞서 다룬 optimization의 경우 모델을 학습하는 과정에 대한 내용이었습니다. 모델을 '학습한다'고 할때 학습이란 train data를 활용하여 결과를 출력하는 모델을 만들었을 때, 그 데이터 안에서 실제 레이블값을 출력하도록 최적의 W값을 찾기 위해 loss 값을 업데이트해 나가는 과정이었습니다.
그러나 우리가 실제로 원하는 것은 단지 train data를 정확하게 알아보는 것이 아니라 새로운 data가 들어왔을 때 이를 얼마나 정확하게 예측할 수 있는냐 하는 문제입니다. 따라서 사실 validation accuracy에만 신경쓰면 되는 문제입니다.
이를 위한 여러 방안들이 있습니다. 사실 regularization 기법은 아니지만 Ensemble 기법도 이와 같은 효과를 낼 수 있습니다. 앙상블 기법은 다음과 같은 2가지 방식이 있습니다.
- 여러 모델을 독립적으로 학습하여 test 결과를 평균(모델별 성능의 차이 완화)
- 하나의 모델의 학습과정에서 성능이 좋았던 부분을 개별 모델로 취급하여 여러 모델처럼 연산(학습률의 변동 완화)
2-2. Drop out
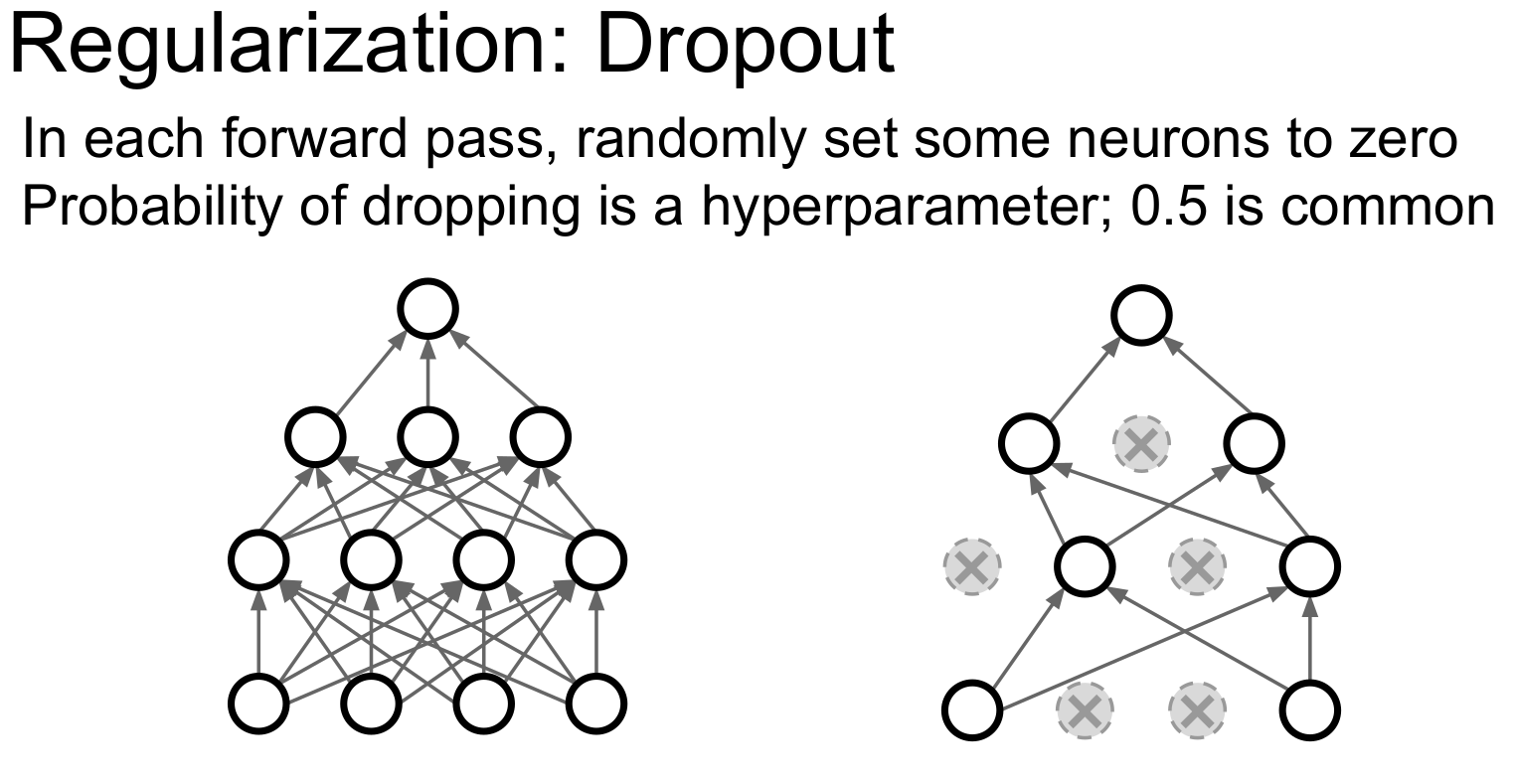


Drop out은 쉽게 말하면 랜덤하게 노드를 꺼주는 기법이라고 할 수 있습니다. 일반적으로 절만을 끈다고 하네요. 일반적으로 FC layer에서 사용하고, Conv에서도 사용할 수 있습니다(채널단위). 기본적으로 두 가지 특징이 있습니다.
- 학습시 특정 feature끼리의 상호작용을 막아줍니다(overfitting 방지)
- 한 모델로 여러 모델을 만들어서 훈련하는 효과(Ensemble)
이때 주의할 점은 뉴런을 일괄적으로 끄고 연산을 시작하는것이 아니라 학습을 해 나가면서 확률값을 계산해 뉴련을 꺼나가기 때문에 이를 위한 연산이 추가됩니다. 따라서 연산시간은 증가한다는 단점이 있습니다.
일반적으로 위의 dropout은 train time의 dropout을 의미합니다. 그렇다면 test time에도 일관되게 진행하면 될까요?
답은 '아닙니다'입니다. 일반화 가능성을 위하여, test time에는 랜덤성을 부여하면 안됩니다. 따라서 dropout 비율(뉴런을 끈 비율, 확률값)을 곱하여 random성을 보정(왜곡을 줄임)하고 훈련뒤의 일반화 가능성을 향상시킵니다.(Average out)
이와 유사한 방식을 이전 단계에서 보았는데요. 맞습니다. 같은 의미로, BN도 좋은 regularizarion 기법입니다. 위에서 살펴보았듯 train단계에서 batch별로 샘플링 후 정규화하여 랜덤성을 부여하고 test단계에서 전체 데이터를 활용하여 정규화하기 때문입니다(Dropout의 Averageout과 유사). 그러나 dropout은 하이퍼파라미터 p를 가지고 있다는 점에서 BN에 비해 유리합니다.
따라서 일반적으로 BN을 수행할 때는 따로 regularization기법을 적용하지 않아도 됩니다. 그러나 overfitting이 될 수도 있으니, 일단 BN을 실시한 후, overfitting의 조짐이 보인다면 Dropout을 추가하는 것도 좋은 선택입니다.
2-3. 그 외 기법들



'모델의 과적합을 막는' 목적을 달성하기 위한 가장 좋은 방법은 dataset의 크기를 늘리는 것입니다. dataset의 절대적인 양이 많은 것이 가장 좋겠지만 비용, 시간, 자료없음 등의 문제로 데이터 스스로 완벽하게 학습하기 위한 조건을 만들기란 매우 어렵습니다(특히 의료데이터). 따라서 regularization을 실시하는데, 주어진 데이터를 변형하여 사용하는 것도 한가지 대안이 될 수 있습니다. 일반적으로 데이터를 뒤집거나, 특정 부분만 자르거나, 색을 조정하는 등의 방식을 사용합니다.
지금까지 살펴본대로 regularization과정에는 다음과 같은 일정한 패턴이 있습니다.
train time : random성을 추가
test time : 정규화, 평균화 하여 랜덤성 제거
e.g
Dropout
Batch Normalization
Data Augmentation
DropConnect
Fractional Max Pooling
Stochastic Depth
3. Transfer learning
우리의 모델을 훈련시킬 만큼의 충분한 데이터가 없다면, 우리의 데이터셋을 이미 학습된 모델에 적용하는 방법도 있습니다. 이를 Transfer learning(전이학습)이라고 합니다.

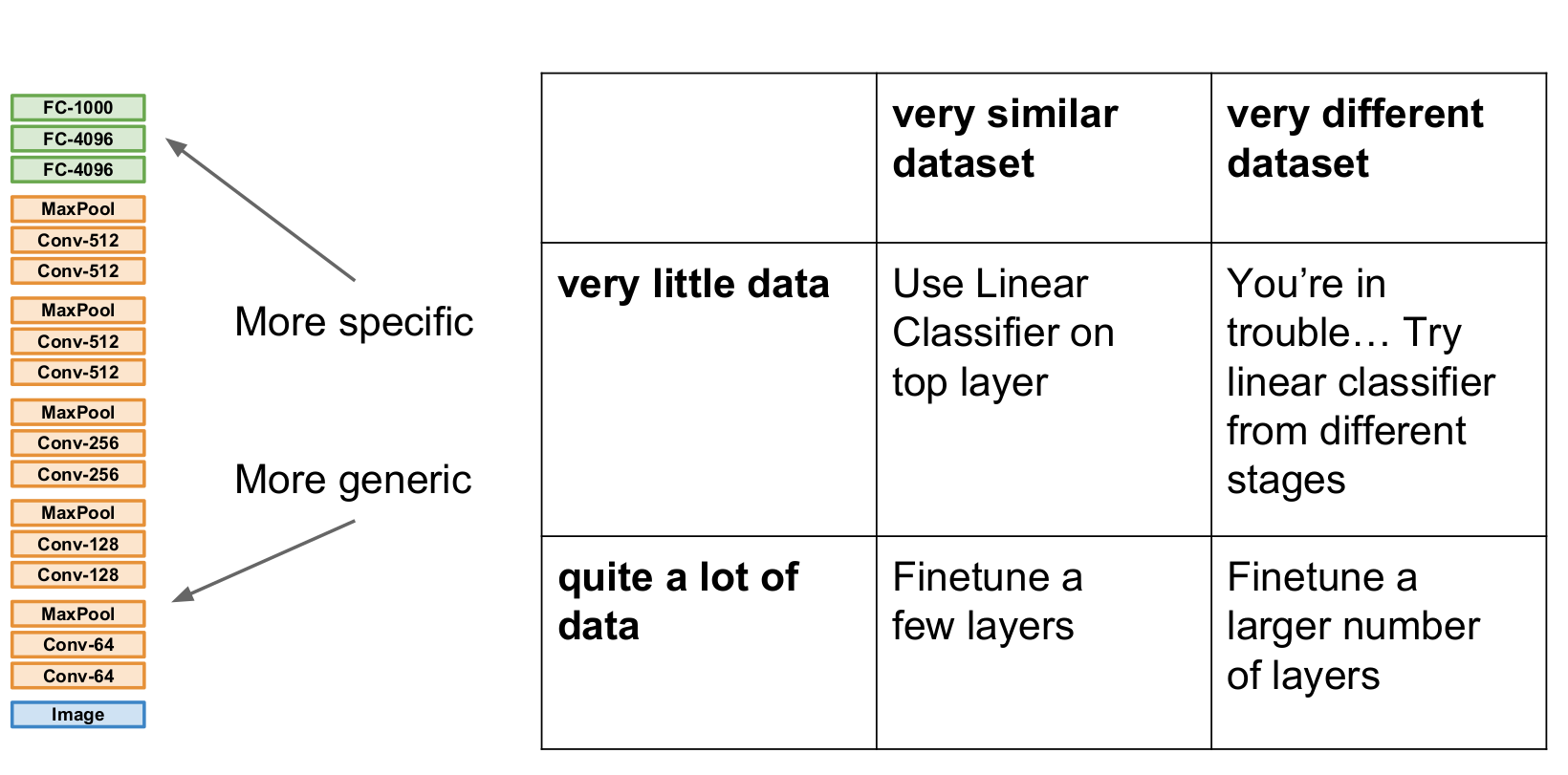
전이학습 시 만약 우리의 데이터가 적다면, 마지막 FC(출력층)의 가중치만 초기화하고 나머지 모든 층의 가중치를 고정하여 학습(fine tuning)시킵니다. 데이터의 크기가 커질수록, 초기화할 layer를 조금씩 늘려가며 학습시킬 수 있습니다. 뭔가 찝찝하지만, 이미 여러 대회나 프로젝트에서 자주 사용되는 방법입니다.
요약하자면
Optimization은 Adam을 사용합시다.
Regularization은 BN을 우선 적용하고, 과적합의 우려가 있을 시 Dropout을 사용합시다.
Transfer learning은 실제 프로젝트에서 많이 사용되니 잘 기억해 둡시다.
해당 글은 스탠퍼드 대학의 CS231n(Convolutional Neural Networks for Visual Recognition)을 정리한 글임을 밝힙니다.
'Note' 카테고리의 다른 글
| Github 업로드 (0) | 2021.06.18 |
|---|---|
| DEEPML(CS231n) Lec.06 Training Neural Networks, Part1 (0) | 2021.02.12 |
| DEEPML(CS231n) Lec.05 Convolutional Neural Networks (0) | 2021.01.31 |
| DEEPML(CS231n) Lec.04_1 Backpropagation (0) | 2021.01.25 |
| DEEPML(CS231n) Lec.04_1_1 What is backpropagation really doing? (0) | 2021.01.24 |